Статически определенные задачи растяжения-сжатия бруса
Наиболее простым и распространенным на практике является случай осевого (центрального) растяжения-сжатия бруса, когда продольные внешние силы действуют вдоль его оси. При этом в статически определимых задачах для определения внутренних усилий N в сечениях бруса достаточно условий статики (2.1):
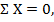
 где под обозначением
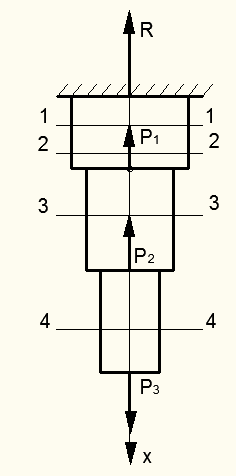
где под обозначением 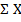 подразумевается алгебраическая сумма всех внешних сил Р, включая реакцию опорного закрепления R, на продольную ось х (рис. 3.1).
подразумевается алгебраическая сумма всех внешних сил Р, включая реакцию опорного закрепления R, на продольную ось х (рис. 3.1).
Расчет элементов растяжения-сжатия ступенчатого бруса производится по этапам в следующей последовательности:
| Рисунок 3.1 – Пример расчетной схемы ступенчатого бруса при растяжении-сжатии |
2) вычисление продольных усилий N по участкам в сечениях бруса;
3) расчет нормальных напряжений σ в сечениях;
4) вычисление абсолютных перемещений ∆l по концам участка бруса и перемещений 𝓌 границ участков относительно его заделки;
5) построение эпюр N, σ, 𝓌 по участкам бруса.
Рассмотрим принципиальную суть указанных этапов.
На первом этапе необходимо определить величину и направление реакции бруса в закреплении. Не зная истинного направления реакции R от внешней нагрузки, направление R принимается произвольно. Если при использовании условия статики (2.1) реакция получилась отрицательной (со знаком минус) то это означает, что истинная реакция имеет обратное направление. На рисунке ранее принятое направление реакции следует изменить на противоположное и в последующих расчетах учитывать положительную величину R со своим реальным направлением.
Последующие этапы 2-4 требуют определения расчетных значений величин N, σ, ∆l по участкам бруса. Участками ступенчатого бруса являются: расстояние от опорного закрепления до ближайшей продольной внешней силы Р или конца ступени бруса; расстояние между внешними силами Р или силой и концом ступени бруса. На рис. 3.1 показан пример выделения расчетных сечений бруса с номерами 1 – 4.
Вычисление продольных усилий 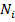 в сечениях бруса (где і – номер сечения) осуществляется с использованием уравнения равновесия (2.1), где под обозначением
в сечениях бруса (где і – номер сечения) осуществляется с использованием уравнения равновесия (2.1), где под обозначением 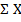 подразумевается алгебраическая сумма проекций всех внешних сил Рі и внутренних усилий
подразумевается алгебраическая сумма проекций всех внешних сил Рі и внутренних усилий 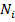 , включая реакцию R, лежащий по одну сторону сечения до отбрасываемой части бруса.
, включая реакцию R, лежащий по одну сторону сечения до отбрасываемой части бруса.
Если на участке бруса задана распределенная нагрузка интенсивности q, то при вычислении 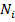 рассчитывается равнодействующая интенсивности нагрузки q·х на участке ее приложения х. Задавая координату х начала и конца приложения распределенной нагрузки, получаем соответствующую равнодействующую этого вида нагружения.
рассчитывается равнодействующая интенсивности нагрузки q·х на участке ее приложения х. Задавая координату х начала и конца приложения распределенной нагрузки, получаем соответствующую равнодействующую этого вида нагружения.
| (3.1) |
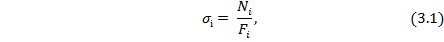
где 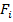 – площадь рассматриваемого поперечного сечения ступени бруса.
– площадь рассматриваемого поперечного сечения ступени бруса.
| (3.2) |

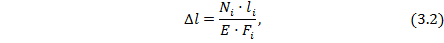
где 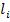 – длина участка ступени бруса; Е – модуль упругости материала бруса.
– длина участка ступени бруса; Е – модуль упругости материала бруса.
| (3.3) |

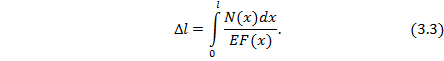
На последнем пятом этапе расчета растяжения-сжатия бруса строятся эпюры N, σ, 𝓌 по участкам бруса.
Под эпюрой подразумевается график зависимостей указанных факторов по длине бруса. Эпюры строятся по одну сторону от вертикальной линии (рис. 3.2). Справа от нее значения элементов растяжения откладываются в масштабе со знаком «+», а слева – элементы сжатия со знаком «-». Эпюры заштриховываются горизонтальными линиями (рис. 3.3).
Если по длине бруса приложена распределенная нагрузка интенсивностью q или требуется учесть силы тяжести ступеней бруса, то элементы его растяжения-сжатия N, σ, 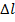 будут зависеть от переменной координаты х. Ее можно отсчитывать по участкам в расчете либо от опорного закрепления бруса, либо от начала его ступеней (см., например, рис. 3.4).
будут зависеть от переменной координаты х. Ее можно отсчитывать по участкам в расчете либо от опорного закрепления бруса, либо от начала его ступеней (см., например, рис. 3.4).
Дата добавления: 2016-10-18; просмотров: 3408;











