Основные уравнения механики деформируемого твердого тела (МДТТ)
I. Зависимости между перемещениями
и деформациями (уравнения Коши)
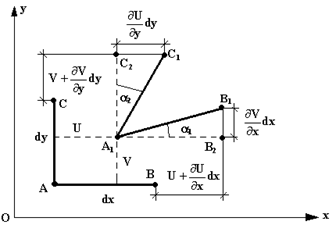 Рис.11.1
Рис.11.1
| Перемещение точки тела в пространстве определяется тремя компонентами вдоль координатных осей: 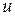 (вдоль оси (вдоль оси 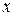 ), ), 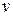 (вдоль оси (вдоль оси 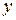 ), ), 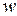 (вдоль (вдоль 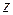 ). Эти перемещения являются функциями координат точки, т.е. ). Эти перемещения являются функциями координат точки, т.е.
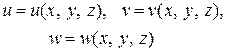
|
Вырежем из тела до его нагружения бесконечно малый прямоугольный элемент с размерами ребер 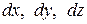 . После нагружения тела он деформируется, т.е. изменяться длины его ребер и прямые углы между гранями.
. После нагружения тела он деформируется, т.е. изменяться длины его ребер и прямые углы между гранями.
На рис.11.1 показаны до деформации тела два ребра этого элемента, длины которых 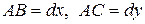 . После деформации т. А переместится в т.
. После деформации т. А переместится в т. 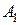 , т.е. получит перемещения
, т.е. получит перемещения 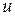 и
и 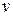 . Точка
. Точка 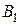 получит перемещения:
получит перемещения: 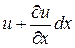 (вдоль оси
(вдоль оси 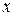 ) и
) и 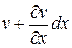 (вдоль оси
(вдоль оси 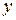 ). Точка
). Точка 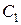 переместится на
переместится на 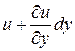 (вдоль оси
(вдоль оси 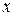 ) и
) и 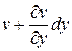 (вдоль оси
(вдоль оси 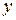 ). Из рис. 11.1 отрезок
). Из рис. 11.1 отрезок 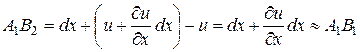 ввиду малости угла
ввиду малости угла 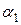 (деформации тела считаются малыми). Относительная деформация ребра АВ вдоль оси
(деформации тела считаются малыми). Относительная деформация ребра АВ вдоль оси 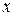 равна
равна
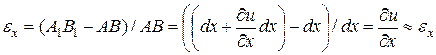 (1)
(1)
Аналогично для ребра 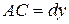 , относительная деформация вдоль оси
, относительная деформация вдоль оси 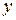 будет
будет 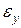 , с учетом
, с учетом 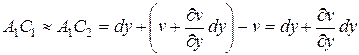
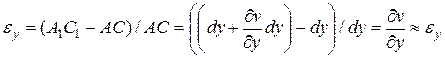 (2)
(2)
Аналогично получим 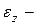 линейную деформацию вдоль оси
линейную деформацию вдоль оси 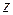 третьего ребра элемента (не показанного на рис.11.1)
третьего ребра элемента (не показанного на рис.11.1)
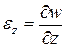 (3)
(3)
Ввиду малости угла 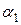 можно записать (из рис.11.1)
можно записать (из рис.11.1)
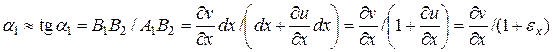 (4)
(4)
Деформации тела малы, поэтому 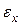 много меньше 1 и
много меньше 1 и 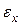 можно не учитывать. Тогда (4) упростится
можно не учитывать. Тогда (4) упростится
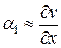 (5)
(5)
Аналогично найдем
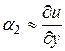 (6)
(6)
Известно, что изменение прямого угла САВ в плоскости 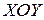 называется сдвигом в плоскости
называется сдвигом в плоскости 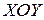 и обозначается
и обозначается 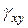 . Следовательно
. Следовательно 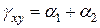 . С учетом (5) и (6) получим
. С учетом (5) и (6) получим
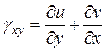 (7)
(7)
Аналогично можно получить 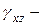 сдвиг в плоскости
сдвиг в плоскости 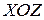 ,
, 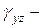 сдвиг в плоскости
сдвиг в плоскости 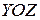 .
.
Итак, деформацию в любой точке тела определяют шесть величин, которые с учетом (1), (2), (3) и (7) можно записать так
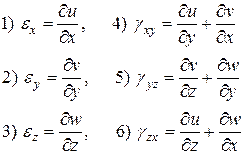 (11.1)
(11.1)
Это и есть уравнения Коши.
II. Условия совместности (неразрывности) деформаций
Представим себе тело, разрезанным на малые параллелепипеды. Если каждый из этих параллелепипедов получит произвольные деформации, то из деформированных параллелепипедов не удастся вновь сложить сплошное тело: во многих точках возникнут щели, пустоты. Следовательно, при деформации тела 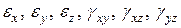 должны быть связаны определенными зависимостями. Получим их.
должны быть связаны определенными зависимостями. Получим их.
Из (11.1) первое дифференцируем дважды по 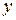 , второе – дважды по
, второе – дважды по 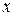 и сложим их
и сложим их
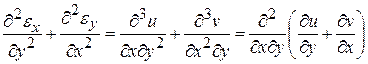 (а)
(а)
Выражение в скобках по 4) из (11.1) равно 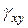 . Тогда
. Тогда
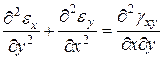 (в)
(в)
Аналогично можно составить еще два соотношения
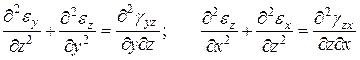 (г)
(г)
Эти соотношения легко записать, используя кольцевую перестановку индексов 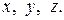
Для однозначности, шесть деформаций должны быть связаны шестью зависимостями.
Продифференцируем три последних уравнения (11.1) так:
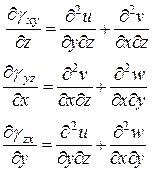
Сложим два первых соотношения и вычтем третье:
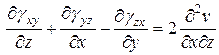
Продифференцируем это уравнение еще раз по 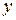 и, учитывая, что по 2) из (11.1)
и, учитывая, что по 2) из (11.1) 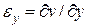 получим
получим
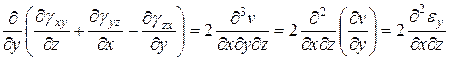 (д)
(д)
Аналогично можно получить еще два уравнения, используя кольцевую перестановку индексов. Итак, окончательно получим шесть уравнений (в), (г) и (д), которые и называют условиями совместности (неразрывности) деформаций или уравнениями Сен-Венана.
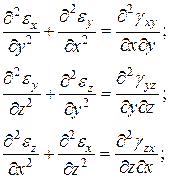 (11.2)
(11.2)
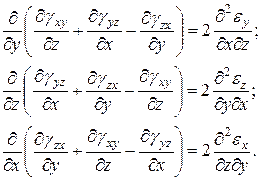
III. Дифференциальные уравнения равновесия
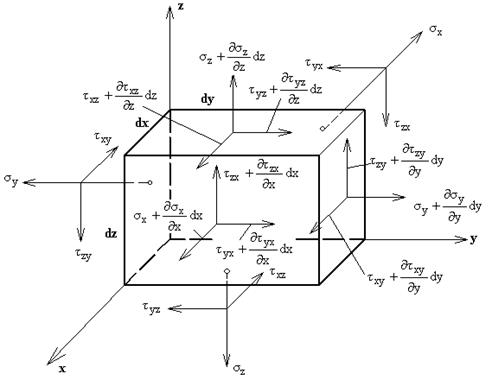
Рис.11.2
Вырежем из нагруженного тела малый прямоугольный элемент с ребрами 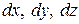 , параллельными осям
, параллельными осям 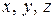 . Со стороны отброшенных частей на элемент действуют напряжения, определяемые тензором напряжений
. Со стороны отброшенных частей на элемент действуют напряжения, определяемые тензором напряжений 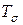 , который в разделе 1 обозначен как формула (1.2). На невидимых гранях (рис.11.2) действуют
, который в разделе 1 обозначен как формула (1.2). На невидимых гранях (рис.11.2) действуют 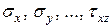 . На рис.11.2 эти напряжения условно вынесены за пределы элемента (чтобы упростить рисунок). В разделе 1 приняты следующие обозначения и правила:
. На рис.11.2 эти напряжения условно вынесены за пределы элемента (чтобы упростить рисунок). В разделе 1 приняты следующие обозначения и правила: 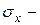 нормальное напряжение вдоль оси
нормальное напряжение вдоль оси 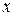 ,
, 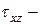 касательное напряжение вдоль оси
касательное напряжение вдоль оси 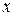 , действующее на площадке, перпендикулярной оси
, действующее на площадке, перпендикулярной оси 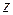 . Аналогично определяются и другие напряжения. Площадки положительны, если внешние нормали к ним направлены вдоль осей. На положительных площадках положительные напряжения направлены вдоль осей
. Аналогично определяются и другие напряжения. Площадки положительны, если внешние нормали к ним направлены вдоль осей. На положительных площадках положительные напряжения направлены вдоль осей 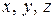 , на отрицательных – против осей.
, на отрицательных – против осей.
Невидимые площадки – отрицательные, поэтому положительные напряжения 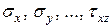 направлены против осей (рис.11.2).
направлены против осей (рис.11.2).
Видимые площадки – положительные и все напряжения на них направлены вдоль осей и имеют добавки по соответствующей координате. Например, на невидимой грани, перпендикулярной оси 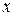 , действуют
, действуют 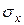 (против оси
(против оси 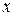 ), а на видимой грани, отстоящей от невидимой на малом расстоянии
), а на видимой грани, отстоящей от невидимой на малом расстоянии 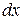 , действуют
, действуют 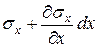 (вдоль оси
(вдоль оси 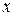 ). Аналогично и на других парах граней.
). Аналогично и на других парах граней.
Кроме напряжений на элемент тела действуют объемные силы, их проекции на координатные оси обозначим: 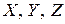 . Эти силы отнесены к единице объема. Объем элемента
. Эти силы отнесены к единице объема. Объем элемента 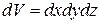 . Тогда силы, действующие в объеме всего элемента, будут равны:
. Тогда силы, действующие в объеме всего элемента, будут равны:
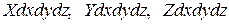 (1)
(1)
Элемент вырезан из нагруженного тела, находящегося в равновесии. Поэтому и малый элемент, под действием всех напряжений, указанных на рис. 11.2 и объемных сил (1), должен быть в равновесии. Следовательно, должны удовлетворятся шесть уравнений статики. Рассмотрим уравнение проекций сил на ось 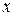 . Каждое напряжение надо умножать на площадь грани, где оно действует, т.е. рассматривать силы на гранях.
. Каждое напряжение надо умножать на площадь грани, где оно действует, т.е. рассматривать силы на гранях.
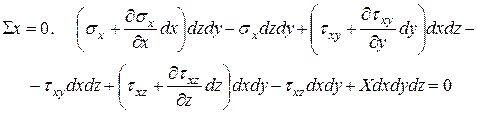
После раскрытия скобок, приведения подобных членов и деления на объем 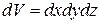 получим
получим
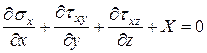 (2)
(2)
Аналогично, составив 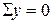 и
и  , можно получить еще два уравнения статики. Проще их записать сразу, используя указанную выше кольцевую перестановку
, можно получить еще два уравнения статики. Проще их записать сразу, используя указанную выше кольцевую перестановку  .
.
В итоге получим три уравнения равновесия малого прямоугольного элемента, вырезанного внутри тела.
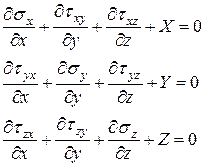 (11.3)
(11.3)
Можно составить еще три уравнения равновесия моментов относительно осей  по выше указанному правилу и убедиться, что они дадут уже известный нам закон парности касательных напряжений (1.3), полученный в разделе 1
по выше указанному правилу и убедиться, что они дадут уже известный нам закон парности касательных напряжений (1.3), полученный в разделе 1
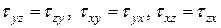
IV. Напряжения на наклонных площадках
(Условия на поверхности)
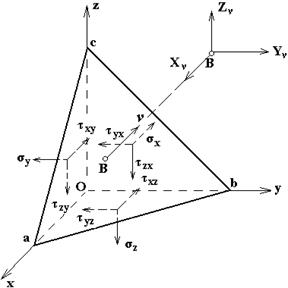 |
Рис.11.3
 с тремя плоскостями, совпадающими с координатными (см. рис. 11.3). Положение в пространстве наклон-ной площадки
с тремя плоскостями, совпадающими с координатными (см. рис. 11.3). Положение в пространстве наклон-ной площадки  определяется нормалью
определяется нормалью 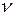 , направляющие конусы которой обозначим так:
, направляющие конусы которой обозначим так:
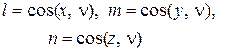 Площадку
Площадку 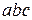 обозначим
обозначим 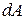 . Невидимые треугольные площадки, перпендикулярные осям
. Невидимые треугольные площадки, перпендикулярные осям 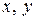 и
и 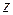 , обозначим и определим так:
, обозначим и определим так:
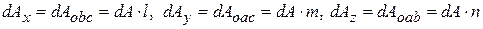 (а)
(а)
На этих невидимых, отрицательных площадках, действуют положительные напряжения, определяемые 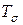 (см. п.III). На наклонной площадке
(см. п.III). На наклонной площадке 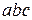 действуют компоненты полного напряжения
действуют компоненты полного напряжения 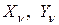 и
и 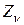 . Под действием всех напряжений, показанных на рис.11.3, тетраэдр находится в равновесии. Умножая напряжения на площадки, составим уравнение статики
. Под действием всех напряжений, показанных на рис.11.3, тетраэдр находится в равновесии. Умножая напряжения на площадки, составим уравнение статики
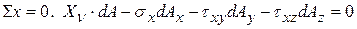 (в)
(в)
Объемные силы 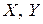 и
и 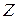 здесь не учитываются, т.к. они пропорциональны объему, который имеет третий порядок малости, а все слагаемые в (в) – второй порядок малости. Подставляя (а) в (в) и сокращая на
здесь не учитываются, т.к. они пропорциональны объему, который имеет третий порядок малости, а все слагаемые в (в) – второй порядок малости. Подставляя (а) в (в) и сокращая на 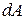 получим
получим
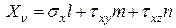 (г)
(г)
Составляя уравнения статики 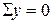 и
и 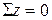 , получим еще два уравнения, которые легко записать, используя кольцевую перестановку
, получим еще два уравнения, которые легко записать, используя кольцевую перестановку 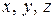 и
и 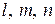 , получим три уравнения равновесия тетраэдра
, получим три уравнения равновесия тетраэдра
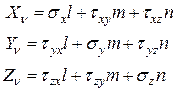 (11.4)
(11.4)
Если площадка 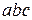 совпадает с поверхностью тела, то
совпадает с поверхностью тела, то 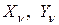 и
и 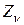 соответствуют компонентам внешней нагрузки. В этом случае уравнения (11.4) называют условиями на поверхности тела. Они связывают внешние напряжения с внутренними в теле.
соответствуют компонентам внешней нагрузки. В этом случае уравнения (11.4) называют условиями на поверхности тела. Они связывают внешние напряжения с внутренними в теле.
Удовлетворение условиям (11.3) и (11.4) является необходимым и достаточным условием равновесия в любой точке тела (внутри и на поверхности).
| <== предыдущая лекция | | | следующая лекция ==> |
| Балка на упругом основании | | | анализ напряженно-деформированного состояния в точке тела |
Дата добавления: 2016-10-18; просмотров: 3650;











