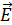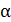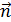Поток вектора напряженности. Теорема Гаусса для ЭСП

В вакууме

Поток вектора напряженности 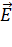электростатического поля через площадку :

,

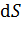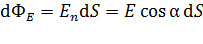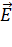где – угол между вектором напряженности и нормалью к площадке 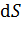(рис. 5).

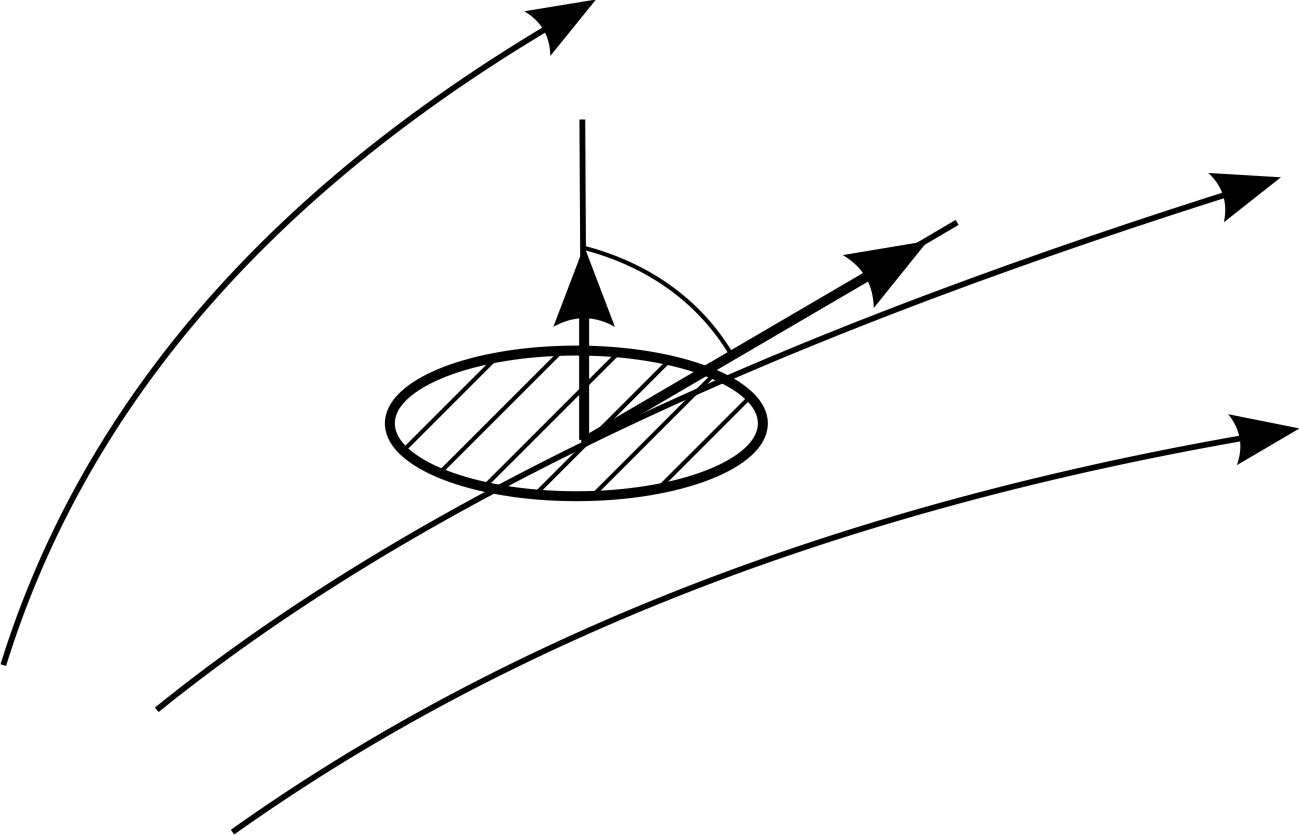
Рис. 5

Поток вектора напряженности 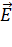через замкнутую поверхность:

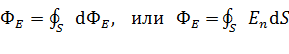. (8)

Теорема Гаусса для ЭСП в вакууме:

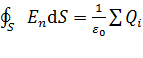. (9)
Поток вектора напряженности ЭСП в вакууме через любую замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на .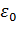

Теорему Гаусса используют для расчета напряженности ЭСП, имеющих симметрию. В таких полях можно выбрать вспомогательную поверхность, для которой просто вычисляется интеграл в левой части теоремы Гаусса (9). Приведем результаты расчета напряженности ЭСП с помощью теоремы Гаусса.

1) Поле сферы радиуса 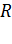, равномерно заряженной по поверхности, на расстоянии от центра сферы:

а) внутри сферы ;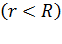

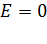б) на поверхности сферы 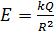, где 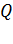– заряд сферы; (10)

в) вне сферы 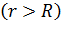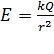. (11)

2) Поле нити (или цилиндра радиуса 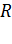для 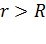) на расстоянии от нити (или от оси цилиндра):

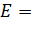
(12)

Здесь 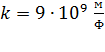; 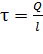– линейная плотность заряда: отношение заряда нити (цилиндра) 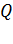к длине нити .

3) Поле плоскости, бесконечной и равномерно заряженной:

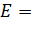
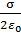, (13)

где – поверхностная плотность заряда: 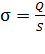– отношение заряда 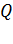к площади плоскости , на которой находится заряд.