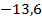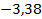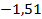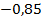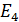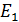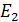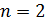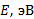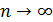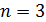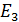Энергетические уровни и спектр излучения атома водорода

Используя уравнение (1) динамики движения электрона в атоме и формулу (2) первого постулата, Бор получил выражение для радиуса 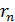-й стационарной орбиты (см. решение задачи 30) в следующем виде:

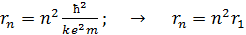, (4)

где 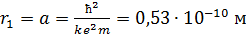– первый боровский радиус.

Формула (4) показывает, что радиусы орбит увеличиваются с ростом квантового числа 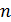пропорционально его квадрату .

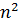Полная энергия 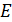электрона в атоме водорода (и в любом другом атоме) равна сумме кинетической энергии 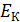электрона и потенциальной энергии 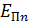его взаимодействия с зарядом ядра (в атоме водорода ):

.

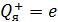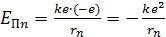Таким образом, величина полной энергии атома водорода в состоянии с главным квантовым числом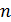

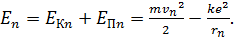(5)

Здесь 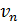– скорость электрона на -й стационарной орбите, она определяется законом динамики (1); 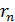– радиус этой орбиты (см. формулу (4)). Расчет энергии атома водорода по формуле (5) (см. решение задачи 32) приводит к следующему результату:

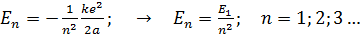. (6)

Здесь 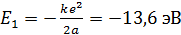– энергия атома водорода в основном состоянии – с квантовым числом 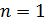.Состояния атома с энергиями 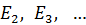, называют возбужденными. Величина 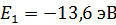является минимальной энергией атома водорода. Максимальная энергия: 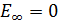, –соответствует ионизации атома путем отрыва электрона от ядра.

Полная энергия атома водорода, согласно формуле (6), отрицательна; это означает, что электрон находится в связанном состоянии. Расчет по формуле (6), где 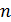– целые числа, дает дискретный набор значений энергии атома, которые называют энергетические уровни. Схема энергетических уровней атома водорода и переходы с излучением энергии показаны на рис. 49. Эти переходы атома из одного состояния в другое

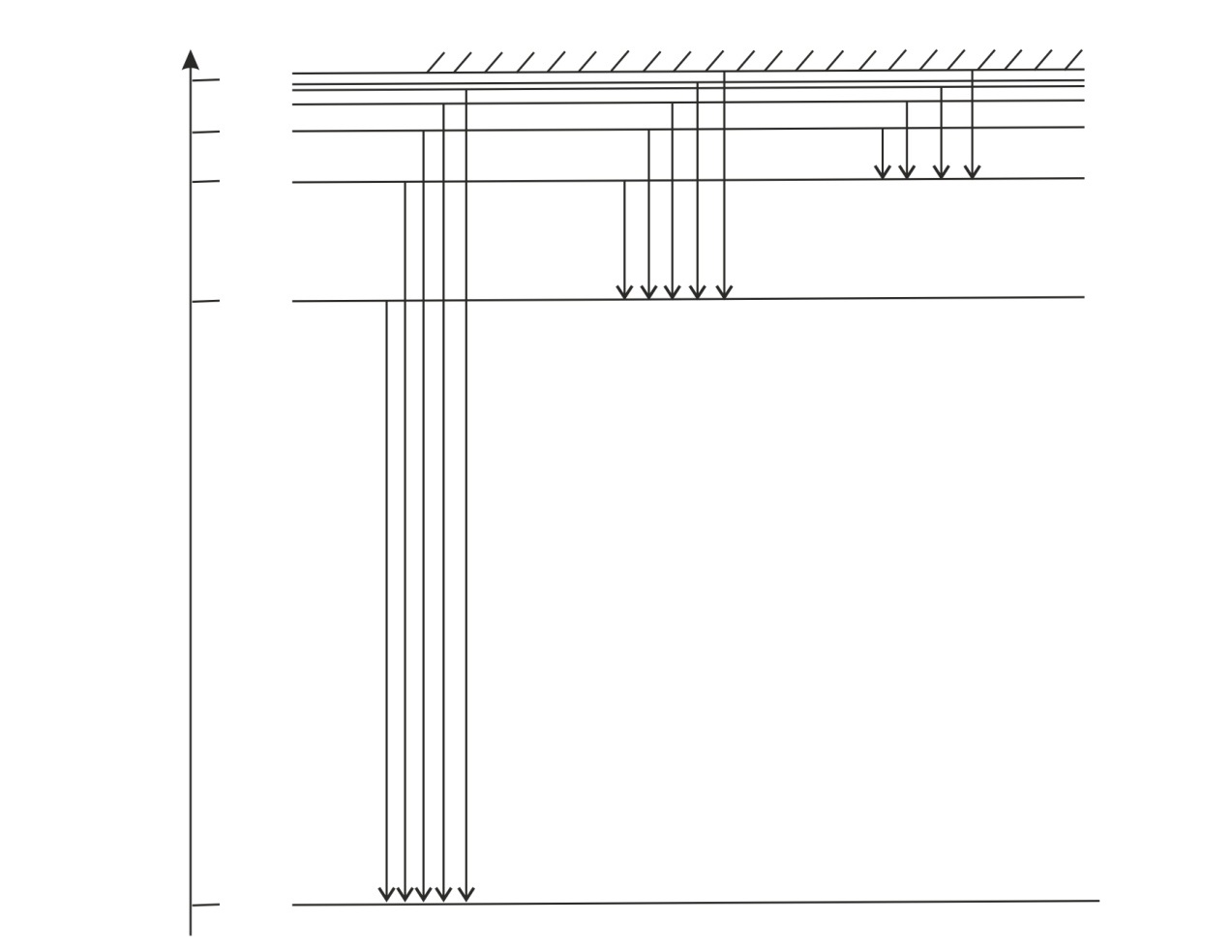
серия Лаймана серия Бальмера серия Пашена Рис. 49

изображены вертикальными линиями, а направление перехода показано стрелкой. Атом переходит в возбужденное состояние при соударении с другим атомом, с заряженной частицей или при поглощении фотона. Время жизни атома в возбужденном состоянии порядка 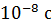. Затем атом самопроизвольно переходит в основное состояние, излучая квант энергии.

Частота 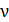и длина волны 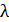излучаемых фотонов определяются вторым постулатом Бора, который, с учетом формулы (6) для энергии атома, запишем в следующем виде:

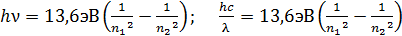. (7)

Формула (7) совпадает с сериальной формулой, полученной ранее экспериментально:

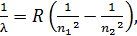(8)

где 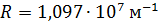– постоянная Ридберга; 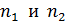– квантовые числа стационарных состояний, причем .

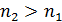По формулам (7) и (8) можно вычислить длины волн спектральных линий всех серий в спектре излучения атома водорода: серия Лаймана ( 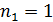) принадлежит ультрафиолетовой области спектра; серия Бальмера ( 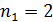) – видимой области; серия Пашена ( 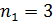) и последующие серии ( 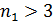) – инфракрасной области спектра.