Правила построения блок–схемы алгоритма
1. выявить исходные данные, результаты и назначить им имена;
2. выбрать порядок решения задачи;
3. разбить решение на этапы;
4. изобразить каждый этап своим блоком.
5. предусмотреть вывод результатов;
6. обеспечить выход (переход к блоку «конец».
3. описание на алгоритмическом языке – это запись алгоритма в аналитическом виде, с использованием некоторых терминов, записанных с строгом порядке.
Виды алгоритмов
1. Линейный алгоритм. Здесь все действия следуют для выполнения строго по порядку, одно за другим.
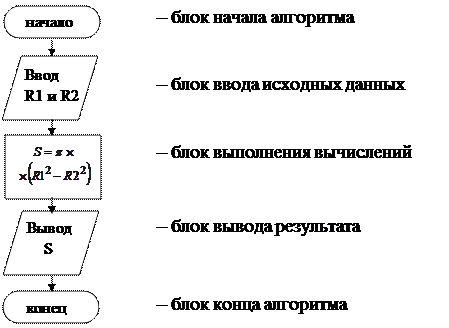 |
 Например. Вычислить площадь кольца, если заданы радиусы внешнего и внутреннего кругов. Вводим обозначения переменных:
Например. Вычислить площадь кольца, если заданы радиусы внешнего и внутреннего кругов. Вводим обозначения переменных: R1 – радиус внешнего круга,
R2 – радиус внутреннего круга,
S – искомая площадь, вычисляемая по формуле
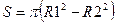 .
.
2. Разветвляющийся алгоритм. Разветвляющимся – называется такой алгоритм, в котором выбирается один из нескольких возможных путей вычислительного процесса. Каждый подобный путь называется ветвью алгоритма. Принципом разветвляющегося процесса является наличие операции проверки условия, которое может быть простым или составным.
Простое условие – это выражение, составленное из двух арифметических или текстовых величин, связанных одним из знаков <, >, £, ³, =, ¹.
Составное условие – это выражение, составленное с помощью логических операций OR, AND, NOT.
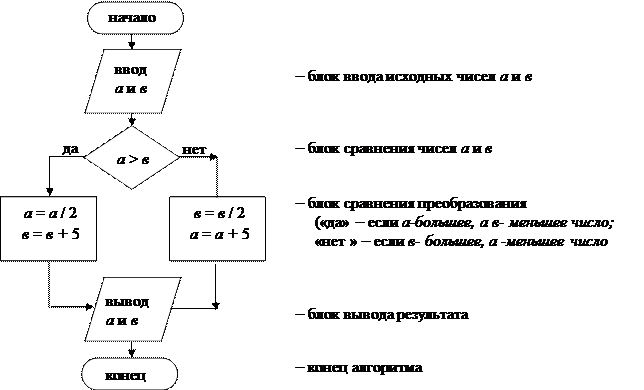
Пример. Из двух данных неравных чисел большее уменьшить вдвое, а меньшее увеличить на 5.
Вводим обозначения чисел а – первое, в – второе число.
 |
3. Циклический алгоритм. Циклическим – называется такой алгоритм, в котором выполнение некоторых действий повторяется конечное число раз с различными данными. Для циклического алгоритма обязательно имеется переменная, которая контролирует число повторений действий (число циклов). По способу проверки числа циклов различают циклы с предусловием и циклы с постусловием и циклы со счетчиком.
Цикл с предусловием – это цикл, в котором проверка окончания цикла выполняется перед действием цикла.
 |
Цикл с постусловием – это цикл, в котором тело цикла выполняется хотя бы один раз перед проверкой окончания цикла.
 |
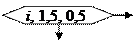
 Цикл со счетчиком – разновидность вышеназванных циклов, в котором переменная цикла изменяется в арифметической прогрессии. Для изображения цикла со счетчиком используется блок внутри
Цикл со счетчиком – разновидность вышеназванных циклов, в котором переменная цикла изменяется в арифметической прогрессии. Для изображения цикла со счетчиком используется блок внутри
которого помещаются начальное и конечное значение переменной цикла и шаг изменения её . Здесь переменная цикла i
будет меняться от 1 до 5 через 0,5 (шаг 0,5).
Пример. Вычислить и вывести все значения функции y = x2 для всех x от 1 до10 с шагом 2.
Обозначение: x – переменная цикла,
y – результат вычисления.
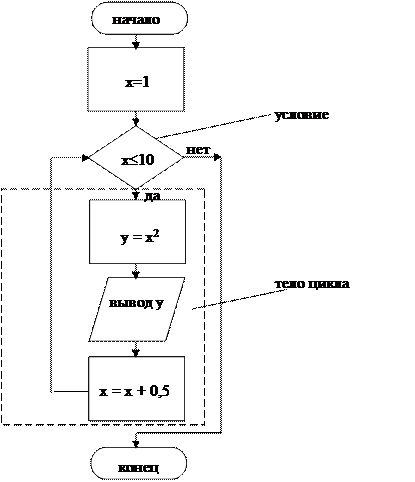 |
a) цикл с предусловием
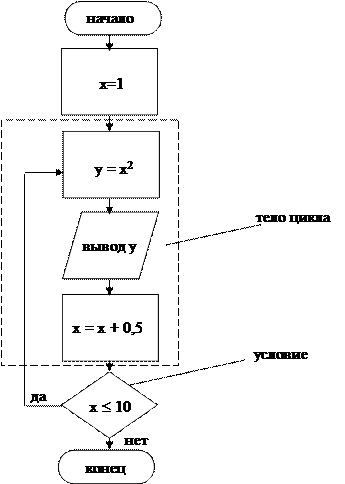 |
б) цикл с постусловием
в) цикл со счетчиком
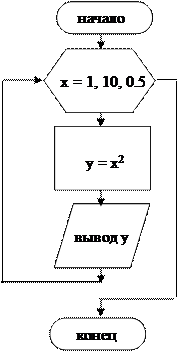 |
| |
Дата добавления: 2021-01-11; просмотров: 547;











