Уравнения синодического движения.

Для нижних планет (1)

Для верхних планет - (2)

Из наблюдений определяются S и .

Законы Кеплера

Кеплер был сторонником учения Коперника и поставил перед собой задачу усовершенствовать его систему по наблюдениям Марса, которые на протяжении 20 лет производил датский астроном Тихо Браге (1546 -1601) и в течение нескольких лет сам Кеплер.

В начале Кеплер разделял традиционное убеждение, что небесные тела могут двигаться только по кругам, и поэтому он потратил много времени на то, чтобы подобрать для Марса круговую орбиту.

После многолетних и очень трудоемких вычислений, отказавшись от общего заблуждения о кругообразности движений, Кеплер открыл три закона планетных движений, которые в настоящее время формулируется следующим образом:

1.Все планеты движутся по эллипсам, в одном из фокусов которых (общем для всех планет) находится Солнце.

2.Радиус-вектор планеты в равные промежутки времени описывает равновеликие площади.

3.Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит.

Как известно, у эллипса сумма расстояний от какого-либо его точки до двух неподвижных точек f1 и f2, лежащих на его оси АП и называемых фокусами, есть величина постоянная, равная большой оси АП (рис 19). Расстояние ПО (или ОА) , где О- центр эллипса называется большой полуосью а, а отношение 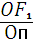= е – эксцентриситетом эллипса. Последний, характеризует отклонения от окружности, е=0.

Рис 19. а) Эллиптическая орбита, б) иллюстрация второго закона Кеплера.

Орбиты планет мало отличаются от окружностей, т.е. их эксцентриситеты невелики. Наименьший эксцентриситет имеет орбита Венера (е=0,007), наибольший – орбита Плутона (е=0,249). Эксцентриситет земной орбиты е=0,017.

Согласно первому закону Кеплера Солнце в одном из фокусов эллиптической орбиты планеты. Пусть на рис.19, а это будет фокус f₁ (С – Солнце ). Тогда наиболее близкая к Солнцу точка орбиты П называется перигелием, а наиболее удаленная от Солнца точка А- афелием. Большая ось орбиты АП называется линией апсид, а линия f₁Р, соединяющая Солнце и планету Р на ее орбите,- радиусом –вектором планеты.

Расстояние планеты от Солнца в перигелии

q = a (1-e), (2.3)

вафелии

Q = a (1 +e). (2.4)

За среднее расстояние планеты от Солнца принимается большая полуось орбиты

А= .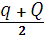

Таким образом, по современным представлениям в солнечной системе, тела двигаются по эллипсам, в одном из фокусов которого находится Солнце.

2.5.2. Лекция №8. Определение характеристик планет Солнечной системы.

Определение расстояния до планет Солнечной системы.

1) Расстояние от Земли до близких крупных тел с твердой поверхностью (Луна, Меркурий, Венера, Марс) успешно применяется радиолокационный или радарный метод.

r = 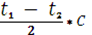c = 29979,2 км/с.

2) Классический метод– определения геоцентрических расстояний – тригонометрический.

Рис 20.Суточный и горизонтальный параллакс светил Земли

Топоцентрическое М₀ положение светила Мположение, видимое с земной поверхности.

Геоцентрическое М_с положение (место)светилаМ –положение, видимое из центра.

Суточный параллакс – угол Р’при светиле между топоцентрическим ОММ₀ и геоцентрическим (ОММ₀) направлениями на светило.

Иначе: суточный параллакс –это угол Р’, под которым со светила виден радиус земной поверхности пункта наблюдения.

В зенитеР’=0. Еслисветило на горизонтеР’=max= Р и называется горизонтальным параллаксом.

Из рисунка видно, что геоцентрическое расстояние:

r = RsinP₀

Величина «Р» измеряется с очень большой погрешностью из – за рефракции.

Земля – сфероид. Поэтому величина R в разных точках различна. Принято при вычислении гелиоцентрических расстояний брать экваториальный радиус R₀ Земли.

Экваториальный параллакс P₀ = P 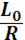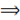r =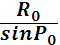

Расстояние определяется в единицах экваториального радиуса Земли R₀. Для вычисления расстояний r в абсолютных единицах надо знать радиус Земли.