Оценивание параметров структурной модели

Косвенный МНК (КМНК) применим в случае точно идентифицируемой структурной модели. Процедура следующая:

1. Структурная модель преобразуется в приведенную форму.

2. Для каждого уравнения приведенной формы обычным МНК оцениваются коэффициенты δ_ij

3. Коэффициенты приведенной модели трансформируются в параметры структурной модели.

Рассмотрим применение КМНК для модели:

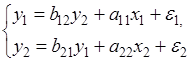
Для построения модели имеем таблицу:

№ п/п
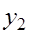
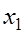
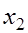
Средние		6,2	2,4	3,4

Приведенная форма модели имеет вид:

где 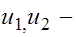случайные ошибки приведенной формы модели.

Для каждого уравнения приведенной формы применим традиционный МНК и определим δ- коэффициенты. Для простоты работаем в отклонениях, т.е. 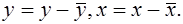Тогда система нормальных уравнений для первого уравнения системы составит:

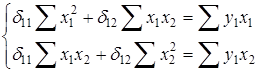
Для приведенных данных система составит:

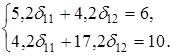
Отсюда получаем первое уравнение ( и аналогично второе):

Перейдем к структурной форме следующим образом: исключим из первого уравнения приведенной формы x₂ , выразив его из второго уравнения приведенной формы и подставив в первое уравнение:

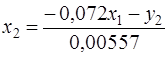
Первое уравнение структурной формы:

Аналогично исключим из второго уравнения x₁ выразив его через первое уравнение и подставив во второе:

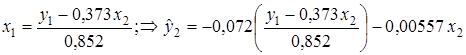
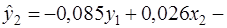второе уравнение структурной формы.

Структурная форма модели имеет вид:

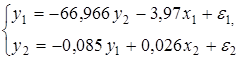
Эту же систему можно записать, включив в нее свободный член уравнения, т.е. перейти от переменных в виде отклонений от среднего к исходным переменным 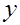и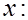

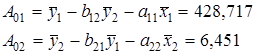
Тогда структурная модель имеет вид:

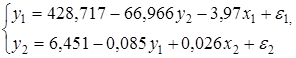
Если к каждому уравнению структурной формы применить традиционный МНК, то результаты могут сильно отличаться. В данном примере будет:

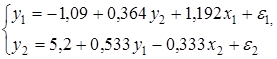
Двухшаговый МНК.ДМНК используется для сверхидентифицируемых систем. Основная идея ДМНК: на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Здесь дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной 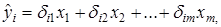и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.

Сверхидентифицируемая структурная модель может быть двух типов:

- все уравнения системы сверхидентифицируемые;

- система содержит также точно идентифицируемые уравнения.

В первом случае для оценки структурных коэффициентов каждого уравнения используется ДМНК. Во втором случае структурные коэффициенты для точно идентифицируемых уравнений находятся из системы приведенных уравнений.

Рассмотрим модель:

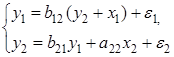
Она получена из предыдущего примера наложением ограничения 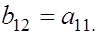Поэтому первое уравнение стало сверхидентифицируемым.

На первом шаге найдем приведенную форму модели. С использованием тех же исходных данных получим систему:

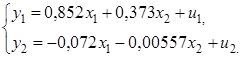
На основе второго уравнения этой системы можно найти теоретические значения для эндогенной переменной 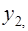т.е. 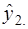Подставим в это уравнение значения 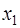и 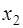в форме отклонений от средних значений, запишем в виде таблицы:

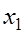
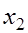
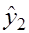
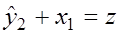
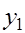
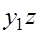
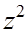
-1,4	-0,4	0,103	-1,297	-2	2,594	1,682
-0,4	-2,4	0,042	-0,358	-1	0,358	0,128
0,6	-1,4	-0,035	0,565			0,319
-0,4	1,6	0,02	-0,38		-0,38	0,144
1,6	2,6	-0,13	1,47		2,94	2,161
					5,512	4,434

После того, как найдены оценки 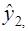заменим в уравнении 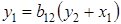фактические значения 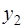их оценками 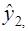найдем значения новой переменной 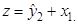Применим МНК к уравнению:

.

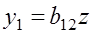Получим:

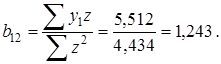
В целом рассматриваемая система будет иметь вид:

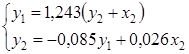
Второе уравнение не изменилось по сравнению с предыдущим примером.

ДМНК является наиболее общим и широко распространенным методом решения системы одновременных уравнений. Для точно идентифицируемых уравнений ДМНК дает тот же результат, что и КМНК.