Понятие о гидродинамическом подобии. Виды подобия (геометрическое, кинематическое, динамическое).

Влияние формы сечения на потери напора.

При вычислении Re потоков в трубах некруглого сечения используют гидравлический радиус R живого сечения:

Формула Дарси-Вейсбаха для потерь напора по длине и коэффициент сопротивления по длине:

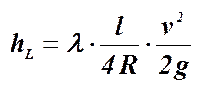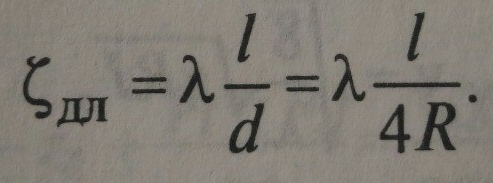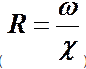, где - гидравлическй радиус – отношение площади живого сечения к смоченному периметру, для круглого сечения R=d/4.

Живое сечение – сечение потока, во всех точках которого линии тока, пересекающие эту поверхность, нормальны к ней.

Смоченный периметр – длина линии, по которой жидкость соприкасается с твердыми поверхностями, ограничивающими поток.

Коэффициент сопротивления системы.

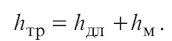
Если трубопровод длиной lимеет на всем протяжении одинако­вый диаметр, а движущаяся по этому трубопроводу жидкость встреча­ет kместных сопротивлений, то суммарная потеря напора определяет­ся по формуле

Пусть все средние скорости выражаются через V₃:

Понятие о гидродинамическом подобии. Виды подобия (геометрическое, кинематическое, динамическое).

Гидравлические исследования проводят в лабораториях на моделях, воспроизводя явления в масштабе. Явление механически подобны, если в них одинаково отношение всех геометрических элементов, плотностей, кинематических параметров и сил.

Гидродинамическое подобие - выполнение всех 3х условий:

· Геометрическое: между соответствующими линейными размерами двух потоков (явлений) существует постоянное отношение (линейный масштаб): Ml=Lн/Lм=const; M_s=M_l² – площади, M_v=M_l³- объемы.

· Кинематическое: для установившегося движения траектории сходственных частиц потоков геометрически подобны, как и линии токов: если частица в натуре за время Тн проходит Iн, то соответственная частица на модели за Тм проходила lм, ориентированный подобно Iн – масштаб времени Мt=Тн/Тм, соответственно масштабы скоростей и ускорений.

· Динамическое: все силы одинаковой природы Рн и Рм, действующую на любую пару сходственных элементов отличаются друг от друга постоянными масштабами Мр.