Примеры применения уравнения Бернулли в технике (расходомер Вентури, трубка Пито – Прандтля).

Уравнение Бернулли является основным законом установившегося движения жидко- сти. Оно позволяет рассмотреть и понять работу ряда устройств, действие которых основано на использовании этого важнейшего закона. Рассмотрим некоторые из устройств.

1. 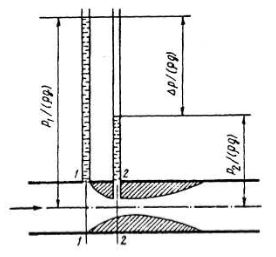Расходомер Вентури. Это дроссельный расходомер, который относится к массовым расхо- домерам переменного перепада давления, отличает- ся простотой конструкции и надежностью работы, так как не содержит никаких подвижных деталей. Расходомер Вентури представляет собой устройст- во, устанавливаемое в трубопроводе и обеспечи- вающее сужение потока. Устройство (рис. 5.7) со- стоит из двух участков – плавно сужающегося (со- пла) и постепенно расширяющегося (диффузора). Скорость потока в суженном месте возрастает, и в соответствии с уравнением Бернулли давление па- дает. На участке между сечениями / – / и 2 – 2 воз- никает перепад давления, который измеряется диф- ференциальным манометром (или парой пьезомет-

ров). Перепад давления определенным образом свя- зан с расходом жидкости. Найдем эту связь. Пусть в

Рис. 5.7. Расходомер Вентури

сечении / – / средняя скорость – v1, давление – p1, площадь сечения S1, a в сечении 2 – 2, т.е. в самом узком месте потока, соответственно v2, р2 и S2. При горизонтальной установке расхо- домера Вентури z1 = z2 и уравнение Бернулли для сечений

/ – / и 2 – 2 имеет вид

p υ21 p

υ22

.(5.42)

+ α1

r g 2g

= + α2 + h1-2

ρ g 2 g

Используя уравнение неразрывности v1S1 = v2S2 и формулу для суммарных потерь на- пора, уравнение (5.42) преобразуем следующим образом:

p - p

υ2 υ2 æS ö υ2

pa pa

1 2 =α

2 - α

1 ç 2 ¸ + x 2 .

r g 2 2 g

1 2g çS ¸ 2 g

è ø

2( p1 - p2 ) é

ρêα2 - α1ç

æ S

ö

ù

¸

ë

è S2 ø

+ x ú û

откуда

n 2 = .

z +

Так как объемный расход

Q = S2V2,

(5.43)

(5.44)

0

то, подставляя выражение (5.43) в уравнение (5.44),

2Dp / ρ

находим

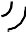
h 2 p r g

3

А υ = 0

z

1 0

Рис. 5.8. Измерение скорости с помощью

Q = μS2

, (5.45)

трубки Пито

где ∆р = p1 - р2 – перепад давления на расходомере;

é

μ = êα2 - α1

ë

-0,5

æ S2

ç

ö

è 1 ø

S

¸

ù

+ x ú

û

– коэффициент расхода.

Значение коэффициента расхода можно подсчитать теоретически, но точнее оно нахо- дится экспериментально, т.е. в результате тарировки расходомера.

Наличие диффузора для дроссельного расходомера не является обязательным. По- следний может быть выполнен в виде сопла. В этом случае увеличивается вихреобразование, возрастает значение коэффициента сопротивления x и, как следствие, снижается значение

коэффициента расхода m.

На практике большое распространение получили дроссельные расходомеры простой конструкции — диафрагменные расходомеры. Диафрагма представляет собой плоский круг- лый диск с осесимметричным отверстием в центре. С одной стороны кромка отверстия обя- зательно острая, а с другой – скошена. Диафрагма зажимается между двумя половинками диафрагменной камеры или просто между фланцами острой кромкой обязательно навстречу потоку. Диафрагменная камера обеспечивает кольцевые зазоры для измерения давления до и после диафрагмы. Если диафрагма зажимается между фланцами, то замер давления — точеч- ный (угловой). По импульсным линиям давление передается к дифманометру-расходомеру, который измеряет перепад давления. Его шкала проградуирована в единицах расхода. Для диафрагменного расходомера формула расхода тоже определяется выражением (5.45), только в этом случае будет другое значение коэффициента расхода m.

2. Трубка Пито. Это устройство предназначено для измерения скорости в любой точ- ке потока. Трубка Пито представляет собой трубку с загнутым концом, устанавливаемым на- встречу течению в точке потока, в которой измеряется скорость (рис. 5.8). Одновременно к отверстию в стенке канала присоединяется пьезометрическая трубка.

Так как уровень жидкости в трубке Пито превышает уровень жидкости в пьезометре на значение скоростного напора в точке А, то, измерив разность уровней h в трубке Пито и пьезометре, имеем

откуда

u 2

h = A ,

2g

2gh

uA = .

Так как трубка Пито возмущает поток, то действительная скорость корректируется коэффициентом скорости j:

2gh

uA = j .

Коэффициент скорости имеет значение j = 1,01…1,03.

2gDhç - 1¸

æρрт

ö

ç

è

ρ

¸

ø

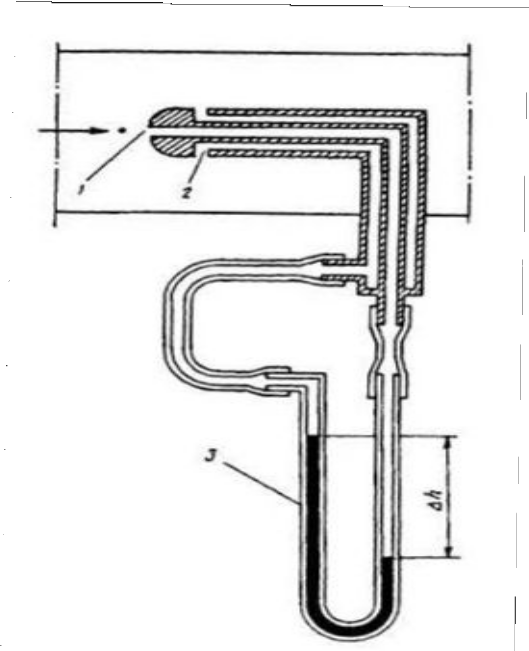Устройство, в котором трубка Пито и пьезометрическая трубка совмещены, называ- ется трубкой Пито-Прандтля(рис. 5.9). К скоростной трубке 1 и пьезометрической трубке 2 трубки Пито-Прандтля подсоединяется дифференциальный манометр 3. Если в дифмано- метр залита ртуть плотностью rрт, а плотность жидкости – r, то

uАд

= j ,

где Dh – разность уровней ртути в трубках дифмано-

метра.

Рис. 5.9. Трубка Пито-Прандтля