Дифференциальный Криптоанализ Высокого Порядка

Многие близкие по содержанию криптоаналитические атаки были выведены из основной DC атаки. Например, атака дифференциального криптоанализа высокого порядка, предлагаемая Лэем в [134], является обобщением дифференциального криптоанализа с использованием повторяющихся текстовых различий (разностей). Лэй определил в [134] текстовую разность как производную дискретной функции, а ее многомерное обобщение как производные высокого порядка.

Определение 5. (Производные [134]) Пусть < S;+ > и <T;+ > будут Абелевыми группами. Для функции 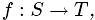производная f в точке 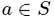определяется как

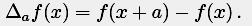
Производная f сама является функцией от S и T, и значит, i-я производная
( i > 1) функции f в точке 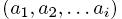может быть определена как

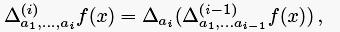
где 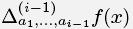является ( i - 1)-й производной функции f в точке 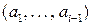. 0-й производная функции f определяется как сама f(x).

Можно отметить следующие свойства производных, которые относятся к функциям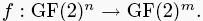

Утверждение 1. [134] Пусть 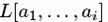будет список всех 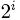возможных линейных комбинаций 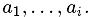Тогда

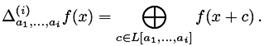
Следствие 1 [134] Производные бинарных функций не зависят от порядка берущейся производной, то есть, для любой перестановки 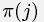индекса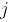

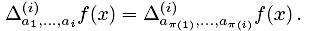
Утверждение 2. [134] Если a_i является линейно зависимым от значений 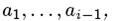то

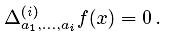
Вероятность дифференциала высокого порядка определяется аналогично определению вероятности дифференциала первого порядка: она является условной вероятностью того, что выходная разность высокого порядка будет принимать ожидаемое значение, при заданной входной разности высокого порядка.

В следующих разделах будут описаны некоторые DC связанные атаки: Square атака, атака невыполнимых дифференциалов и дифференциальные атаки (1-го порядка), применительно к реальным блочным шифрам. Должно допускаться, что фиксированный ключ используется для шифрования всех известных/выбранных плайнтекст/шифротекстов, по меньшей мере, в однотекстовой структуре [24].

[1]⁾ Булева функция - функция, аргументы которой, равно как и сама функция, принимают значения из двухэлементного множества {0,1}. Б.ф. возникли при математической постановке задач логики и были названы по имени Дж. Буля (G. Boole), положившего начало применению математики в логике.

[2]⁾ Это известное определение коэффициента корреляции для двоичных векторов (сообщений) в виде отношения разности числа совпадающих двоичных элементов и числа несовпадающих элементов к их общему числу.