Дифференциальный криптоанализ
Ускоренные атаки
В этом разделе мы рассмотрим атаки, названные ускоренными, так как они для своей реализации требуют меньших вычислительных затрат чем рассмотренные выше атаки универсального типа. Они были найдены (построены) в свое время для вполне определенных шифров и затем уже распространены (развиты) для многих других. Большинство таких атак удалось применить к вариантам блочных шифров с уменьшенным числом циклов. Они позволили обнаружить новые и важные взаимодействия между процессами шифрования/расшифрования и алгоритмами планирования ключей.
Наиболее известные ускоренные атаки включают:
- Линейный Криптоанализ Мацуи [152, 154] и его варианты с использованием многократных приближений Калиски и Робшоу [106];
- Дифференциальный Криптоанализ Бихама и Шамира [24] и вариантные атаки с использованием дифференциалов Лэя [135], дифференциалов высокого порядка Лэя [134] и усеченных дифференциалов Кнудсена [114], Square атаки Даймера и др. [59], атаки на основе невыполнимых дифференциалов Бихама и др.[18], Бумеранг-атаки Бирюкова и Вагнера [223], ускоренные Бумеранги Келси и др.[108], прямоугольные атаки Бихама и др.[20].
- Дифференциально-Линейные атаки Лангфорда и Хэллмана [138];
- Скользящие атаки и усовершенствованные скользящие атаки Бирюкова и Вагнера в [33, 34];
- Атаки со связанным ключом Бихама [13] и Кнудсена [112, 113];
- Атака Дэвиса, разработанная Дэвисом и Марфи [63], и Несюрьективные атаки Риджмена и др.[194];
- Атаки разбиения (Partitioning attacks) Харпеса [86], Келси и др.[109];
- 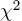 атаки Воденея [221], Кнудсена и Мэйера [122];
атаки Воденея [221], Кнудсена и Мэйера [122];
- Нелинейный Криптоанализ Шимояма и Канеко [212], Кнудсена и Робшоу [123];
- Интерполяционные атаки Якобсона и Кнудсена [99].
Сейчас мы кратко охарактеризуем некоторые из них.
2.2.1. Линейный Криптоанализ (Linear cryptanalysis)
Открытие линейного криптоанализа обычно приписывают M. Мацуи [113], Тем не менее, первое появление идеи можно обнаружить в статье A. Tardy-Corfdir и H. Gilbert [62].
Основной смысл этого, да и многих других ускоренных методов криптоанализа, состоит в замене сложного (как правило, не поддающегося строгому математическому описанию) криптографического преобразования некоторым статистическим аналогом (эквивалентом), для которого уже можно выполнить если уж не математический, то статистический анализ.
Сущность линейного криптоанализа состоит в поиске и использовании линейного соотношения между некоторыми битами открытого текста, некоторыми битами зашифрованного текста, и некоторыми ключевыми битами, выражающегося в виде равенства (линейного отношения):
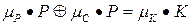 , (1)
, (1)
где 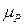 ,
, 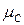 ,
, 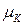 - маски, а символ "·" обозначает скалярное произведение над
- маски, а символ "·" обозначает скалярное произведение над 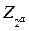 , a - размерность соответствующего текста или ключа (в битах).
, a - размерность соответствующего текста или ключа (в битах).
Это уравнение должно поддерживаться с вероятностью p достаточно "далекой" от 1/2 для того, чтобы позволить нападающему найти отличие между блочным шифром и произвольной перестановкой. Эффективность атаки и оценивают так называемым смещением линейного отношения, под которым понимают "расстояние" от p до 1/2:
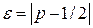 . (2)
. (2)
Поскольку скалярное произведение векторов над полем 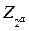 можно рассматривать как булеву функцию[1]) (набору двоичных значений сообщения или ключа, определяемому маской, ставится в соответствие их сумма по модулю два, т.е. булева функция f задается отображением
можно рассматривать как булеву функцию[1]) (набору двоичных значений сообщения или ключа, определяемому маской, ставится в соответствие их сумма по модулю два, т.е. булева функция f задается отображением 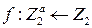 ), то полезным оказывается также привлечение понятия корреляции (коэффициента корреляции) между двумя булевыми функциями.
), то полезным оказывается также привлечение понятия корреляции (коэффициента корреляции) между двумя булевыми функциями.
Определение 1. Пусть 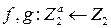 Корреляция между функциями
Корреляция между функциями
f и g это число, определяемое соотношением
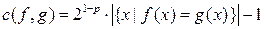 , (3)
, (3)
где 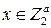 ,
, 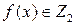 [2]).
[2]).
Основная задача при построении атаки линейного криптоанализа состоит в том, чтобы идентифицировать (обнаружить) отношения, поддерживаемые достаточно высоким смещением. С этой целью, криптоаналитик сначала вычисляет смещение всех нетривиальных линейных отношений на уровне S-блоков: для 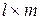 S-блока, он вычисляет смещение для всех пар масок
S-блока, он вычисляет смещение для всех пар масок 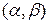 , где
, где 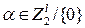 , а
, а 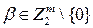 :
:
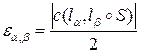 , (4)
, (4)
где булева функция 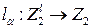 определяется как
определяется как
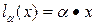 ,
,
а булева функция 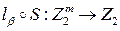 - определяется как
- определяется как
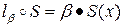 .
.
Здесь 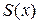 - m битовый выход S-блока при воздействии на его вход l битового слова (вектора) x.
- m битовый выход S-блока при воздействии на его вход l битового слова (вектора) x.
Связь коэффициента корреляции со смещением в виде выражения (4) получена, исходя из того, что для S-блоков рассматриваются линейные отношения (уравнения), связывающее его входы и выходы:
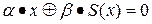 .
.
Далее, если обозначить вероятность выполнения последнего равенства через 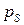 , то очевидно, что
, то очевидно, что
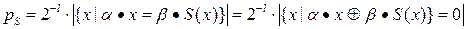 ,
, 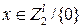 .
.
Тогда, в соответствии с определением коэффициента корреляции, имеем
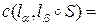
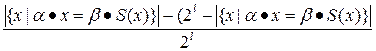 =
=
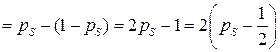 .
.
Остается воспользоваться обозначением (2), которое в данном случае принимает вид
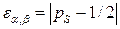 .
.
В итоге приходим к результату (4).
Наибольший интерес, естественно, представляют линейные отношения с высоким смещением.
Нападающий пытается объединить линейные аппроксимации отдельных
S-блоков нескольких циклов, так чтобы биты промежуточных состояний в окончательном результате исключались. Если суммируется t линейных отношений, соответствующих смещениям 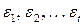 , то смещение
, то смещение 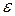 полученного линейного отношения можно вычислить, используя накапливающую лемму (piling-up lemma):
полученного линейного отношения можно вычислить, используя накапливающую лемму (piling-up lemma):
Теорема 1 (накапливающая лемма). Пусть (xi), i = 1, . . . , t будут независимыми случайными переменными, каждая из которых принимает значение 0 с вероятностью pi и 1 с вероятностью 1 - pi. Тогда вероятность того, что x1Å x2 Å, . . . , Å xt = 0 есть
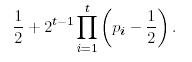
В результате, если мы используем t линейных отношений, которые являются независимыми, то смещение для их суммы есть
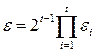 . (5)
. (5)
Алгоритм распознавания оказывается очень простым:
(1) Накапливается определенное число плайнтекст/шифртекстовых пар
(Pi, Ci).
(2) Оценивается смещение 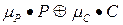 для всех пар (Pi, Ci). Пусть
для всех пар (Pi, Ci). Пусть 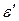 будет предполагаемым смещением. Если
будет предполагаемым смещением. Если 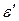 будет близким к
будет близким к 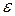 , принимается решение, что пара (Pi, Ci), сгенерирована блочным шифром. Если
, принимается решение, что пара (Pi, Ci), сгенерирована блочным шифром. Если 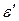 близко к 0, то принимается решение, что использована произвольная перестановка. Определение порога принятия решения является статистической задачей проверки гипотез.
близко к 0, то принимается решение, что использована произвольная перестановка. Определение порога принятия решения является статистической задачей проверки гипотез.
Для того, чтобы процесс распознавания был эффективным, числом m пар
(Pi, Ci), должно быть больше, чем 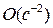 .
.
Заметим, что это атака с известным открытым текстом, так как может быть использована любая пара (Pi, Ci) (тем не менее, выбранные варианты открытого текста могут уменьшить сложность атаки, смотри [97]).
Распознаватель (алгоритм) может быть использован для того, чтобы извлекать ключевые биты, используя 2R-атаку (будет рассмотрена в дальнейшем): нападающий обнаруживает хорошее линейное уравнение, поддерживающее целый шифр, кроме первого и последнего цикла:
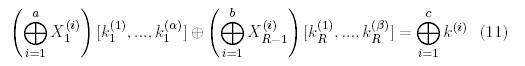 . (6)
. (6)
где 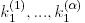 являются цикловыми ключевыми битами, необходимыми для оценки
являются цикловыми ключевыми битами, необходимыми для оценки 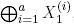 , а
, а  ключевыми битами необходимыми для оценки
ключевыми битами необходимыми для оценки 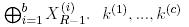 являются другими цикловыми ключевыми битами, которые используются между циклом 2 и R - 1-м циклом.
являются другими цикловыми ключевыми битами, которые используются между циклом 2 и R - 1-м циклом.
Итак, получаются множество пар 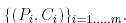 . Затем проверяются (угадываются) биты
. Затем проверяются (угадываются) биты 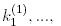
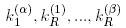 путем оценки смещения левой стороны (4) для этих m пар. Наиболее вероятным кандидатом для ключевых битов
путем оценки смещения левой стороны (4) для этих m пар. Наиболее вероятным кандидатом для ключевых битов 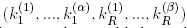 является тот, который имеет самое высокое предполагаемое смещение; второй наиболее вероятный кандидат - со вторым самым высоким предполагаемым смещением, и так далее. Заметим, что одновременно угадывается (получается) и значение
является тот, который имеет самое высокое предполагаемое смещение; второй наиболее вероятный кандидат - со вторым самым высоким предполагаемым смещением, и так далее. Заметим, что одновременно угадывается (получается) и значение 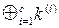 . После этого для каждого кандидата (от наиболее вероятного до менее вероятного) с помощью полного перебора определяются остальные ключевые биты, пока правильный ключ не будет обнаружен.
. После этого для каждого кандидата (от наиболее вероятного до менее вероятного) с помощью полного перебора определяются остальные ключевые биты, пока правильный ключ не будет обнаружен.
Заметим, что необходимо, чтобы число a + b битов во входной и выходной масках было малым, так как число 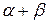 цикловых ключевых битов, на которых строится догадка, должно быть достаточно небольшим.
цикловых ключевых битов, на которых строится догадка, должно быть достаточно небольшим.
С точки зрения разработчика, одной из стратегий, чтобы эффективно защититься от линейного криптоанализа является достижение верхней границы смещения для всех линейных отношений S-блоков. Эта верхняя граница смещения определяется с помощью 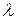 -параметра для p ´ q S-блока S, который определяется как
-параметра для p ´ q S-блока S, который определяется как
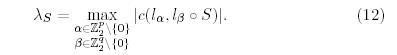 (7)
(7)
Грубо говоря, 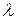 -параметр равняется удвоенному максимальному смещению S-блока.
-параметр равняется удвоенному максимальному смещению S-блока.
Нападающий должен аппроксимировать много S-блоков, чтобы получить линейное отношение для целого шифра, что затрудняет обнаружение хорошего линейного отношения. Следовательно, максимизация числа линейных ветвлений (linear branch number) [146, 46] линейного преобразования  также хорошая стратегия для разработчика, чтобы защититься от линейной атаки. Для определения этого понятия нам потребуется еще два понятия.
также хорошая стратегия для разработчика, чтобы защититься от линейной атаки. Для определения этого понятия нам потребуется еще два понятия.
Определение 2. Блочный Хэмминговый вес Wi(x) (block Hamming weight) битовой строки x при разделении x на блоки из i битов, есть количество не равных нулю блоков.
Определение 3. Число линейных ветвлений (linear branch number) линейного преобразования  определяется как
определяется как
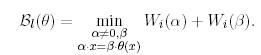
Длина блоков, рассматриваемая в этом контексте, равняется размеру
S-блоков. Если мы описываем  используя матрицу M:
используя матрицу M:  (x) = Mx, то линейное число ветвлений может быть эквивалентно выражено как
(x) = Mx, то линейное число ветвлений может быть эквивалентно выражено как
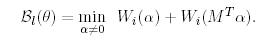
Дифференциальный криптоанализ
Дифференциальный криптоанализ (DC) введен Э. Бихамом и A. Шамиром в 1991г. [19].
Основная идея атаки состоит в обнаружении отличий шифра от случайной перестановки, проявляющихся при прохождении через циклы преобразований шифра пар плайнтекстов, имеющих фиксированную (одну и ту же) разность (дифференциал). Атака становится эффективной, как только удается установить плайнтекстовое различие (разность) 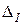 , которое результируется (переходит) в шифртекстовое различие
, которое результируется (переходит) в шифртекстовое различие 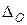 с некоторой достаточно высокой вероятностью.
с некоторой достаточно высокой вероятностью.
Дифференциальный криптоанализ, таким образом, основан на установлении плайнтекстовых различий 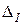 , которые результируются (переходят при шифровании) в шифротекстовые различия
, которые результируются (переходят при шифровании) в шифротекстовые различия 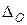 с некоторой "высокой" вероятностью p.
с некоторой "высокой" вероятностью p.
Под "высокой" подразумевается вероятность "значительно более высокая, чем 1/2n". Фактически, 1/2n - средняя вероятность того, что некоторый дифференциал ( 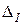 ,
, 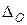 ) поддерживается для случайной перестановки Pn.
) поддерживается для случайной перестановки Pn.
Аналогично случаю линейного криптоанализа, такой дифференциал обнаруживается сначала путем оценки вероятностей всех возможных дифференциалов для каждого S-блока, а затем предпринимается попытка соединить эти дифференциалы вместе для того, чтобы, в конце концов, получить дифференциал ( 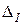 ,
, 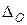 ) для целого шифра. Таблица, содержащая вероятности, связывающие пары входов и выходов различных S-блоков названа
) для целого шифра. Таблица, содержащая вероятности, связывающие пары входов и выходов различных S-блоков названа 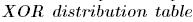 (мы ее будем называть таблицей распределении XOR разностей). С использованием этих таблиц можно определить параметр, измеряющий сопротивляемость S-блоков дифференциальному криптоанализ, как это было сделано для линейного криптоанализа:
(мы ее будем называть таблицей распределении XOR разностей). С использованием этих таблиц можно определить параметр, измеряющий сопротивляемость S-блоков дифференциальному криптоанализ, как это было сделано для линейного криптоанализа:
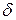 -параметр для q ´ r S-блока S есть вероятность наилучшего дифференциала (разности) через этот S-блок.
-параметр для q ´ r S-блока S есть вероятность наилучшего дифференциала (разности) через этот S-блок.
Более формально
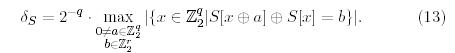 (6)
(6)
Кроме того, вводится понятие числа дифференциальных ветвлений (differential branch number) [146, 46] линейного преобразования. Оно в рассматриваемом контексте играет ту же роль что и число линейных ветвлений при линейном криптоанализе.
Определение 4. differential branch number линейного преобразования  определяется как
определяется как
Bd(q) = 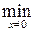 Wi(x) + Wi(q (x)).
Wi(x) + Wi(q (x)).
Алгоритм различения состоит в следующем:
(1) Шифруется m пар (Pi, 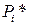 ) открытых текстов с Pi Å
) открытых текстов с Pi Å 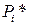 =
= 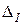 .
.
(2) Среди соответствующих пар (Ci, 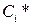 ) зашифрованных текстов, подсчитывается числом N таких, для которых Ci Å
) зашифрованных текстов, подсчитывается числом N таких, для которых Ci Å 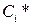 =
= 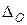 . Затем, пользуются проверкой гипотез для получения решения: если N/m близко к p, то принимается решение, что функция, производящая зашифрованные тексты является примером блочного шифра. Если N/m близко к
. Затем, пользуются проверкой гипотез для получения решения: если N/m близко к p, то принимается решение, что функция, производящая зашифрованные тексты является примером блочного шифра. Если N/m близко к 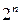 , то принимается решение, что это были произвольные перестановки.
, то принимается решение, что это были произвольные перестановки.
Сложность данных алгоритма есть 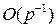 . Так как должны быть выбраны пары с данным различием, то это атака с выбранными открытыми текстами. Тем не менее, если имеется достаточное число открытых текстов (доступно), то нападающий может обнаружить достаточное число пар с необходимым различием среди них. Как это имеет место при линейном криптоанализе, дифференциальный распознаватель (алгоритм) может быть использован в контексте lR атаки.
. Так как должны быть выбраны пары с данным различием, то это атака с выбранными открытыми текстами. Тем не менее, если имеется достаточное число открытых текстов (доступно), то нападающий может обнаружить достаточное число пар с необходимым различием среди них. Как это имеет место при линейном криптоанализе, дифференциальный распознаватель (алгоритм) может быть использован в контексте lR атаки.
Дата добавления: 2016-09-26; просмотров: 2674;











