Фундаментальные последовательности рациональных чисел

И их свойства

Определение. Последовательностью рациональных чисел называется всякое отображение .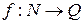

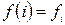– ый член этой последовательности.

Определение. Последовательность рациональных чисел называется сходящейся в поле Q к числу в том и только том случае, когда Число 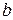называется пределом данной последовательности. Обозначать этот факт будем 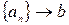при или .

Определение. Последовательность называется фундаментальной последовательностью рациональных чисел (ф.п.р.ч.) в том и только том случае, когда .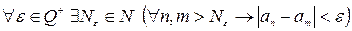

Свойство 1 ф.п.р.ч.Любая сходящаяся в поле рациональных чисел последовательность является фундаментальной последовательностью рациональных чисел.свойства

Доказательство.

Пусть сходится к b. Тогда

.

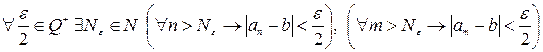Оценим :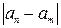

.

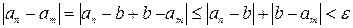В силу произвольности 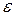также произвольно, следовательно, фундаментальность доказана.

что и требовалось доказать.

Определение. Подпоследовательностью последовательности называется последовательность 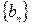такая, что 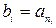, причем отображение 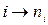является монотонно возрастающей функцией для каждого натурального .

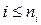Теорема 1.Любая подпоследовательность сходящейся последовательности рациональных чисел является сходящейся к тому же числу последовательностью рациональных чисел.

Доказательство.

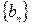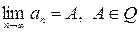Пусть подпоследовательность последовательности , где . Возьмем произвольное рациональное число , тогда в силу сходимости найдется такое 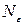, что 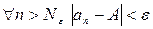. Пусть k – произвольное натуральное число, большее 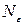. Тогда 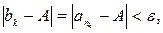т.к. 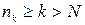. Следовательно, последовательность 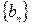сходится к A.

что и требовалось доказать.

Свойство 2 ф.п.р.ч. Любая подпоследовательность фундаментальной последовательности рациональных чисел является фундаментальной последовательностью рациональных чисел.

Доказательство.

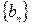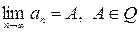Пусть подпоследовательность последовательности , где . Возьмем произвольное рациональное число , тогда в силу сходимости найдется такое 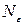, что 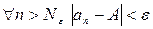. Пусть k – произвольное натуральное число, большее 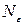. Тогда 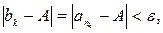т.к. 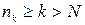. Следовательно, последовательность 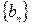сходится к A.

Докажем фундаментальность подпоследовательности 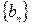фундаментальной последовательности . Из того, что - ф.п.р.ч. следует, что 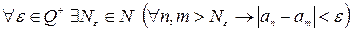. Пусть x, y – произвольные натуральные числа, большие 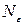. Оценим :

.

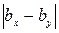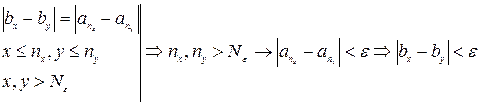Таким образом, фундаментальность 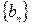доказана.

что и требовалось доказать.

Замечание. Любая постоянная последовательность является фундаментальной (в силу ее сходимости).

Определение. Последовательность рациональных чисел называется ограниченной рациональным числом 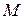в том и только том случае, когда .

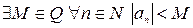Свойство 3 ф.п.р.ч. Любая фундаментальная последовательность рациональных чисел является ограниченной.

Доказательство.

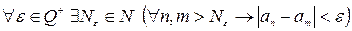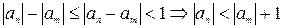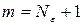Пусть - ф.п.р.ч. Тогда . Возьмем . Зная, что . Поскольку последнее неравенство выполняется для любых , в том числе и для . Следовательно, . Мы нашли число, ограничивающее все члены последовательности по абсолютной величине, начиная с номера 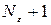. Тогда, полагая 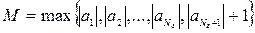, получим .

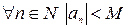что и требовалось доказать.