Упорядоченность поля рациональных чисел.

Определение. Поле 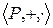называется упорядоченным, если кольцо 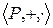является упорядоченным.

Теорема 5.Поле рациональных чисел упорядоченное.

Доказательство.

Рассмотрим подмножество 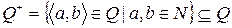. Легко проверить аксиомы положительного конуса.

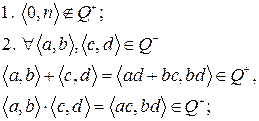
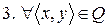возможен один из трех случаев:

§ ,

§

§ .

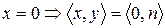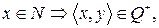
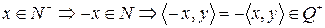что и требовалось доказать.

Следствие 1. Бинарное отношение < на Q, определенное по правилу 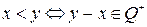является строгим линейным порядком и удовлетворяет свойствам 1.-6. (см. теорему об упорядоченных кольцах).

Следствие 2. Бинарное отношение 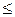на Q, определенное по правилу 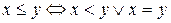является линейным порядком.

Архимедовская расположенность поля рациональных чисел.

Теорема 6.Поле рациональных чисел архимедовски расположенное, т.е. выполняется аксиома Архимеда: .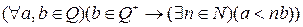

Доказательство.

Пусть .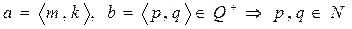

Заметим, что .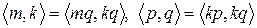

Поскольку кольцо целых чисел является архимедовски расположенным, имеем: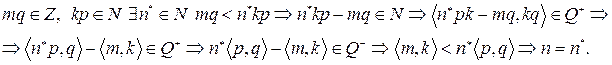

что и требовалось доказать.

Теорема 7. Поле рациональных чисел является всюду плотным.

Доказательство.

Пусть 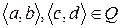. Для определенности положим, что 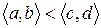. Покажем, что элемент 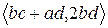лежит между указанными элементами, т.е. 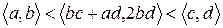. Докажем каждое из неравенств отдельно.

(?)

(?)

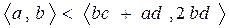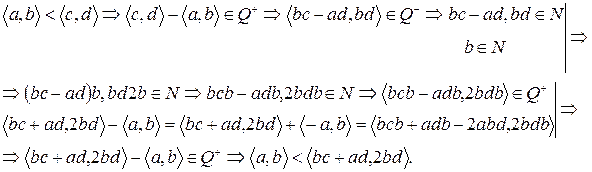
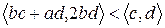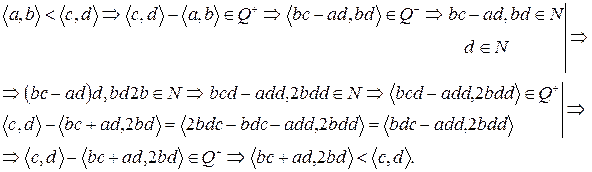
что и требовалось доказать.

Лекция 7.