Архимедовская расположенность кольца целых чисел.
Теорема 16. Кольцо целых чисел является архимедовски расположенным, т.е. выполняются следующее условие (аксиома Архимеда): 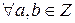 , где
, где 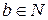 ,
, 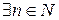 такое, что a<nb.
такое, что a<nb.
Доказательство.
Пусть a и b- натуральные числа. Докажем справедливость утверждения методом математической индукции по 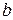 .
.
1. База индукции b=1.
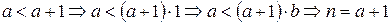 .
.
2. Индуктивное предположение.
Пусть верно для 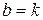 , т.е.
, т.е. 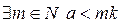 .
.
3. Проверим для 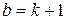 , т.е.
, т.е. 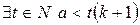 (?)
(?)
Тогда 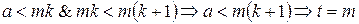 .
.
Пусть теперь 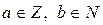 . Возможны случаи:
. Возможны случаи:
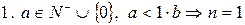 ,
,
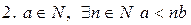 (доказано выше).
(доказано выше).
что и требовалось доказать.
Теорема 17. Кольцо целых чисел не является всюду плотным.
Доказательство.
Поскольку 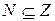 , а
, а 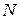 не является всюду плотным, то и
не является всюду плотным, то и 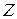 также всюду плотным не будет.
также всюду плотным не будет.
что и требовалось доказать.
Лекции 5-6.
Построение множества рациональных чисел.
Рассмотрим множество 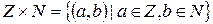 , на котором введем отношение
, на котором введем отношение 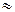 по следующему правилу:
по следующему правилу:
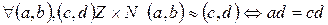
Теорема 1. Отношение ≈ на множестве 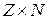 есть отношение эквивалентности (рефлексивно, симметрично, транзитивно).
есть отношение эквивалентности (рефлексивно, симметрично, транзитивно).
Доказательство.
Отношение ~ рефлексивно (?)
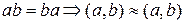 .
.
Отношение ~ симметрично (?)
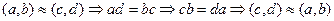 .
.
Отношение ~ транзитивно (?)
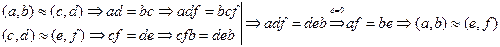 .
.
что и требовалось доказать.
Поскольку ≈ - есть отношение эквивалентности на множестве 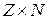 , имеют место классы эквивалентности:
, имеют место классы эквивалентности:
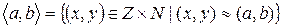 .
.
Определение. Рациональными числами назовем элементы фактормножества 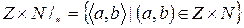 .
.
Дата добавления: 2022-04-12; просмотров: 228;











