Абсолютная величина целого числа и его свойства.
Определение. Абсолютной величиной (или модулем) целого числа a называется число 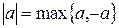 .
.
Замечание.Данное определение корректно, поскольку множество {a,-a} – ограничено, следовательно, есть наибольшее.
Свойства модуля:
(доказательство самостоятельно)
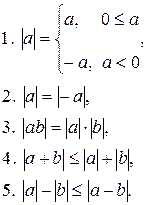
Доказательство.
Свойства 1 и 2 следуют из определения.
Свойство 3. Для доказательства равенства 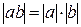 рассмотрим все возможные случаи:
рассмотрим все возможные случаи:
1) 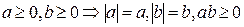 . Из этих соотношений получаем:
. Из этих соотношений получаем:
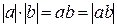 .
.
2) 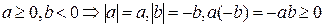 . Отсюда имеем:
. Отсюда имеем: 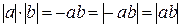 .
.
3) 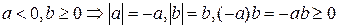 . Отсюда получаем:
. Отсюда получаем: 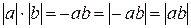 .
.
4) 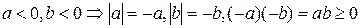 . Отсюда следует:
. Отсюда следует: 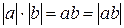 .
.
Таким образом, во всех возможных случаях выполняется равенство 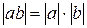 .
.
Свойство 4. Из 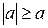 и
и 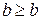 получаем:
получаем: 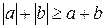 .
.
Из 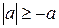 и
и 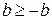 получаем:
получаем: 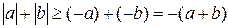 .
. 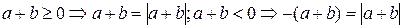 .
.
В обоих возможных случаях имеем: 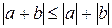 .
.
Свойство 5. Из 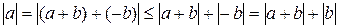 следует соотношение
следует соотношение 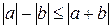 .
.
что и требовалось доказать.
Теорема о делении с остатком.
Теорема 15. 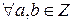 , где b≠0, существует и при том единственная пара целых чисел
, где b≠0, существует и при том единственная пара целых чисел 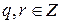 такая, что
такая, что 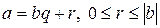 .
. 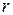 назовем остатком при делении a на b, q – неполным частным.
назовем остатком при делении a на b, q – неполным частным.
Доказательство.
Существование (?)
Проведем методом математической индукции в 3-ей форме.
1. База индукции.
Рассмотрим множество 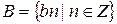 . Очевидно, это множество непустое и не ограничено сверху. Для любого элемента
. Очевидно, это множество непустое и не ограничено сверху. Для любого элемента 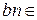 В верна теорема о делении с остатком в разделе существования, поскольку b≠0, bn=bn+0, где
В верна теорема о делении с остатком в разделе существования, поскольку b≠0, bn=bn+0, где 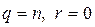 ,0≤
,0≤ 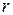 <
< 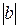 .
.
2. Индуктивное предположение.
Предположим, что для произвольного целого числа z данная теорема справедлива, т.е.z = bq+r, где 0≤r< 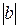 .
.
3. Проверим справедливость данного утверждения для числа z – 1.
z = bq+r 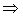
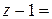 bq+(r–1), где0≤r<
bq+(r–1), где0≤r< 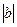 .
.
Рассмотрим возможные случаи:
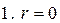
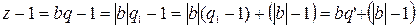 , где
, где 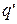 - неполное частное,
- неполное частное, 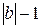 - остаток, причем 0≤
- остаток, причем 0≤ 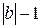 <
< 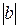 .
.
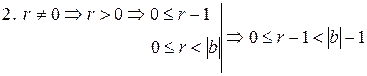 . Тогда q, r–1 – искомая пара чисел для
. Тогда q, r–1 – искомая пара чисел для 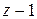 и
и 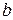 .
.
Существование доказано.
Единственность (?)
Методом от противного. Пусть 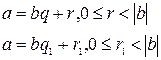 . Тогда
. Тогда 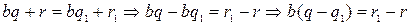 . Учитывая, что
. Учитывая, что 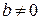 , рассмотрим следующие случаи:
, рассмотрим следующие случаи:
1. 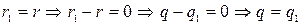 .
.
2. 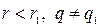 . Тогда
. Тогда 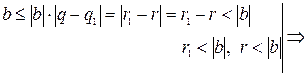
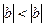 - противоречие. Следовательно, такой случай невозможен.
- противоречие. Следовательно, такой случай невозможен.
3. 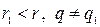 . Невозможен, доказательство аналогично 2.
. Невозможен, доказательство аналогично 2.
Таким образом, из трех случаев возможен только один 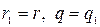 . Единственность доказана.
. Единственность доказана.
что и требовалось доказать.
Дата добавления: 2022-04-12; просмотров: 236;











