Упорядоченность кольца целых чисел.

Теорема 9.Кольцо целых чисел 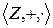является упорядоченным кольцом с положительным конусом N.

Доказательство.

Множество N является непустым подмножеством целых чисел, удовлетворяющих всем аксиомам положительного конуса.

что и требовалось доказать.

Следствие 1. Отношение < на множестве 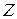, определенное по правилу 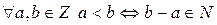, является строгим линейным порядком и выше указанным удовлетворяет свойствам 1.-6.

Следствие 2. Отношение 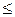на множестве 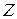, определенное по правилу 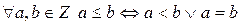, является линейным порядком.

Три формы метода математической индукции для целых чисел.

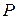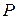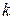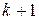Теорема 10 (І форма): Если утверждение о целых числах верно для целого числа и из верности утверждения для произвольного целого числа , большего , следует верность утверждения для числа , то утверждение верно для каждого целого числа, большего или равного .

.

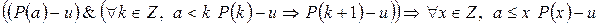Доказательство.

Проведем методом от противного. Предположим, что 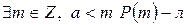. Рассмотрим множество 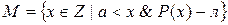. 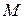ограничено снизу числом . 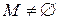, т.к. 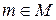. Тогда, по теореме 13, 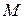имеет наименьший элемент 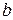. Покажем, что 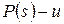, где 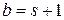. Предположим, что 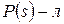, причем 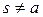(так как иначе 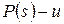). Тогда 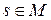, но это противоречит тому, что 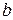- наименьший в 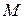. Согласно индуктивному предположению 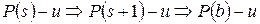. Последнее противоречит условию 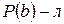. Значит, предположение неверно, и .

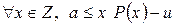что и требовалось доказать.

Теорема 11 (ІІ форма): Если утверждение 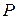о целых числах верно целого числа и для произвольного целого числа 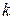, большего , из верности утверждения 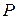для всех целых чисел 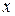таких, что 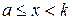, следует верность утверждения для числа 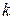, то утверждение верно для каждого целого числа, большего или равного .

.

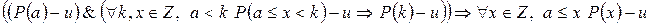Доказательство.

Проведем методом от противного. Предположим, что 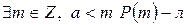. Рассмотрим множество 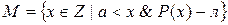. 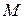ограничено снизу числом . 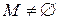, т.к. 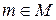. Тогда, по теореме 13, 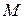имеет наименьший элемент 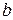. Покажем, что 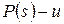, где 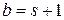. Предположим, что 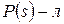, причем 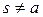(так как иначе 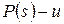), следовательно, 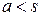. Тогда 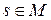, но это противоречит тому, что 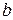- наименьший в 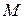. Согласно индуктивному предположению 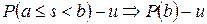. Последнее противоречит условию 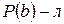. Значит, предположение неверно, и .

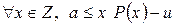что и требовалось доказать.

Теорема 12 (ІІІ форма). Если утверждение 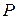о целых числах верно для каждого целого числа некоторого непустого неограниченного сверху подмножества множества целых чисел и из верности утверждения 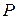для произвольного целого числа 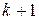следует верность утверждения для числа 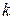, то утверждение верно для каждого целого числа.

.

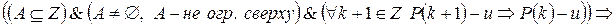
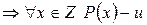Доказательство.

Проведем методом от противного. Предположим, что 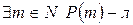. Рассмотрим множество 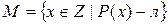. 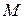ограничено сверху любым элементом из 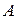. 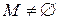, т.к. 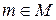. Тогда, по теореме 14, 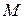имеет наибольший элемент , причем 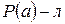. Рассмотрим элемент 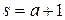. 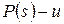, т.к. в противном случае, не будет наибольшим в 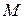. Согласно индуктивному предположению 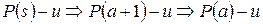, но это противоречит условию 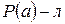. Таким образом, предположение неверно, и .

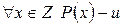что и требовалось доказать.