Кластеризация морфологических множеств

Генерируемые на морфологических таблицах морфологические множества вариантов систем имеют сложную неоднородную внутреннюю структуру. Выявление закономерностей строения исследуемых множеств позволяет более эффективно решать основные задачи по поиску, прогнозированию и планированию рациональных систем. Предварительная кластеризация морфологических множеств с учетом особенностей структуры и свойств вариантов систем помогает во многих задачах преодолеть проклятие размерности, отсеять неинтересные для исследователя варианты систем. Можно выделить два способа формирования классов. Первый способ заключается в том, что классы формируются в процессе конкретного исследования. Второй способ предполагает предварительное задание классов исследователем. При проведении исследований, связанных с выявлением новых классов, применяются методы, позволяющие проводить иерархическое упорядочение морфологических множеств на основе мер сходства; определять подмножества вариантов, наиболее сходных между собой по различным признакам и свойствам; выявлять классы, содержащие наиболее типовые или наиболее оригинальные варианты. Если отряды классов задаются предварительно исследователем, то решается задача идентификации. Цель идентификации — распознавание синтезируемого на морфологической таблице варианта системы и отнесение его к тому или иному классу с учетом решающих правил. Таким образом, осуществляется сортировка синтезируемых вариантов по классам.

Результаты кластеризации в конечном итоге определяются способом описания альтернатив в морфологической таблице, правилом вычисления меры сходства, методом построения иерархической классификации, структурой морфологической таблицы, способом задания классов при решении задачи идентификации.

Решая задачи исследования морфологических множеств на основе методов кластерного анализа, следует различать три существенно отличающихся способа описания альтернатив в морфологической таблице. Способ описания альтернатив обусловливает метод вычисления меры сходства между синтезируемыми вариантами систем. Можно выделить три способа описания альтернатив и соответствующие им правила определения сходства между вариантами.

Первый способ описания каждой альтернативы предполагает указание только ее наименования, например описание альтернативы может быть представлено в виде А_ij. При втором способе описания каждая альтернатива имеет наименование и экспертные оценки, указывающие степень сходства со всеми другими альтернативами, принадлежащими одной обобщенной функциональной подсистеме. Третий способ представления предусматривает указание для каждой альтернативы классификационных признаков. Указанная для характеристики альтернатив информация используется при вычислении мер сходства между синтезируемыми вариантами. Вычисление мер сходства осуществляется по различным правилам.

При первом способе описания альтернатив в виде наименований А_ij меры сходства между двумя вариантами S' и S" вычисляются по известной формуле

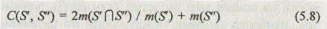
с учетом следующих правил:

• число элементов множества, образующего вариант системы S¢ или S¢¢', равно числу альтернатив А_ij, входящих в данное множество;

• число пересечений элементов двух множеств S' и S" равно числу одинаковых пар альтернатив А¢_lm и А¢¢_lm, принадлежащих соответственно вариантам S' и S", т. е.

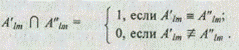
При втором способе описания альтернатив на основе экспертной оценки их степени сходства друг с другом расчет меры сходства между двумя вариантами S¢ и S" системы определяется по формулам:

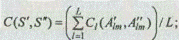
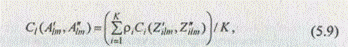
где С_l (A¢_lm, А¢¢_lm) — экспертное интегрированное значение меры сходства пары альтернатив, принадлежащих l-и обобщенной функциональной подсистеме;

L — число обобщенных функциональных подсистем, образующих вариант системы;

С_i (Z¢_ilm, Z¢¢_ilm) — экспертное значение меры сходства пары альтернативпоi-му классификационному признаку или критерию качества;

r_i — весовой коэффициент, определяющий вклад в меру сходства i-ro признака или критерия;

К — число признаков или критериев,по которым описаны свойства альтернатив А¢_lm и A¢¢_lm.

При третьем способе описания вариантов синтезируемых систем определение меры сходства между вариантами осуществляется по выражению (5.9). Вариант системы здесь описан множеством значений признаков Z_ilm = {0,1}. Значение признака Z_ilm равно единице в описании альтернативы А_lm, если признак присутствует в ней, в противном случае Z_ilm = 0.

Рассмотрим строение морфологических множеств относительно иерархических классификаций. Первоначально исследуем морфологическое множество, включающее варианты, альтернативы которых описаны в соответствии с первым способом, т. е. простым указаниемих наименований. При проведении исследований данного типа целесообразно определить наиболее приемлемый метод классификации. Критерием для отбора метода кластеризации может являться хорошая интерпретируемость полученных результатов, т. е. достижение высокой адекватности между моделью-классификацией и реальной системой-прототипом. Проанализируем шесть наиболее простых и распространенных методов иерархической классификации: медианы, максимальных значений, минимальных значений, средней группы, центроиды, Уорда. Осуществим кластеризацию морфологического множества, систематизированного морфологической таблицей (табл. 5.11). Исходное морфологическое множество (табл. 5.12) сформировано алгоритмом лексикографического упорядоченияальтернатив.

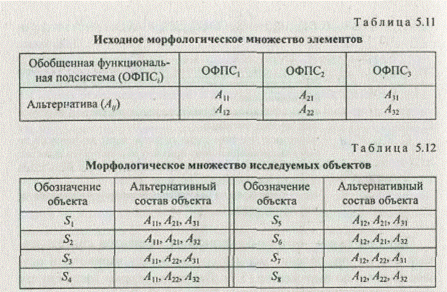
Объекты морфологического множества состоят из трех функциональных подсистем. С учетом выражения (5.8) и относящихся к нему правил формируется матрица мер сходства вариантов:

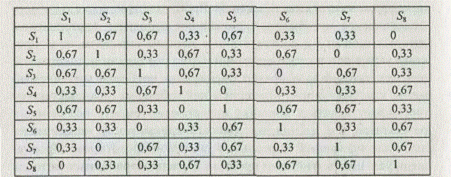
Обработка матрицы сходства шестью указанными методами позволяет получить шесть иерархических классификаций (дендрограмм). Анализ дендрограмм (рис. 5.5) показывает, что все методы, кроме метода максимальных значений, дают качественно сходные классификации. В то же время количественные значения уровней сходства у дендрограмм, построенных методами медианы и средней группы, существенно отличаются от дендрограмм, построенных другими методами.

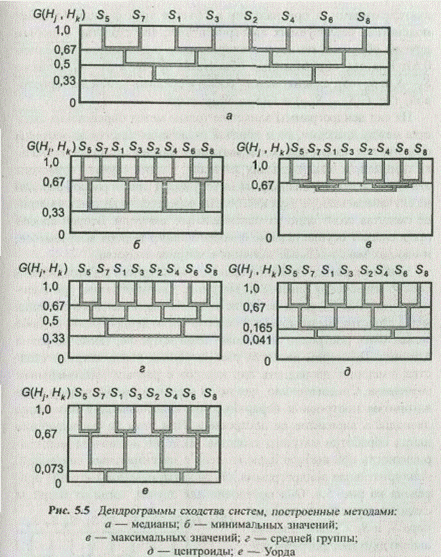
При этом более верные результаты дают методы медианы и средней группы. Действительно, пары объектов S₅—S₇, S₁—S₃, S₂—S₄, S₆—S₈ сходны между собой двумя альтернативами, а при наличии в объекте трех функциональных подсистем, реализуемых альтернативами, его сходство с любым другим объектом по двум альтернативам оценивается значением 0,67. Классы, образованные объектами S₅—S₇ и S₁—S₃, а также S₂—S₄ и S₆—S₈, сходны между собой в среднем одной альтернативой, т. е. G(S_5-7, S_1-3) = G(S_2-4, S_6-8) = 0,5.

На вид дендрограммы влияет не только метод определения сходства между классами, но и порядок извлечения классов из матрицы сходства для тех случаев, когда указанные матрицы содержат несколько одинаковых максимальных значений. В этих случаях возможны два способа извлечения классов из матрицы. Первый способ основан на случайном выборе двух классов, на пересечении которых в матрице сходства стоит одно из максимальных значений. Второй способ предполагает осуществление одновременного выбора всех классов, имеющих максимальные значения в матрице сходства.

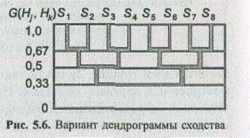
Наиболее распространен в практике кластерного анализа первый способ извлечения классов из матрицы. Таким образом, при наличии в матрице сходства не единственного максимального значения меры сходства анализируемых классов число дендрограмм, которое может быть построено на основе такой матрицы, также не равно единице. Примером является рассмотренная ранее матрица сходства, имеющая двенадцать пар классов с равным максимальным значением. Следовательно, для такой матрицы уже на первом шаге алгоритма построения иерархической классификации возможны двенадцать вариантов ее построения. При этом на последующих шагах обработки матрицы сходства также не исключена многовариантность при выборе пары классов с максимальным значением. Альтернативная дендрограмма для рассматриваемой матрицы приведена на рис. 5.6. Она построена для случая, когда из матрицы сходства первой извлекалась пара S₁ и S₂.

Сравнительный анализ двух дендрограмм показывает, что их структуры идентичны, однако наблюдается перегруппировка классов на всех иерархических уровнях сходства.

С учетом проведенного анализа можно рекомендовать для исследования морфологических множеств методы медианы и средней группы.

Проанализируем рассматриваемое морфологическое множество на предмет наличия в нем наиболее типичных и оригинальных вариантов. Для этого рассчитаем правый собственный вектор матрицы сходства:

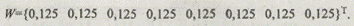
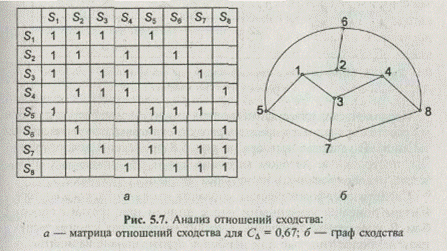
В полученном векторе все значения одинаковы. Следовательно, морфологические множества, содержащие варианты систем, представленные альтернативами, описанными в виде наименований, не содержат наиболее типовых или наиболее оригинальных вариантов. Полученный результат наглядно иллюстрируется графом сходства (рис. 5.7), который построен для максимального порогового значения отношения сходства С_D = 0,67.

Построение матрицы включения вариантов систем, входящих в рассматриваемое морфологическое множество, показало, что она идентична матрице сходства, т. е. симметрична относительно главной диагонали. Это подтверждает наличие особой специфики у морфологических множеств, полученных методом комбинирования альтернатив.

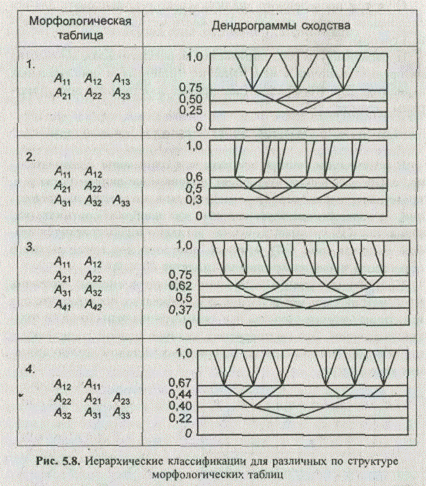
Иерархическая классификационная структура морфологических множеств определяется прежде всего строением морфологической таблицы. В качестве примера на рис. 5.8 приведены дендрограммы, построенные методом медианы для морфологических множеств, сгенерированных на четырех различных таблицах.

Свойства морфологических множеств изменяются, если альтернативы описаны указанными ранее вторым или третьим способом. В этом случае в морфологических множествах удается выделить наиболее типовые или наиболее оригинальные варианты.