Отношения мер сходства, включения и иерархии

Отношения мер сходства (различия), включения и иерархии позволяют при обработке множеств исследуемых объектов выявлять наиболее интересные закономерности строения анализируемых множеств. В общем случае под отношением понимается пара <А, М>, где М— множество, на котором отношение определено, а А — подмножество пар М x М, для которых это отношение выполнено. Множество М называется областью задания отношения А.

Отношения мер сходства и иерархии исследуются на основе матриц сходства множества рассматриваемых объектов, а отношения мер различия и включения исследуются на основе матриц мер различия и включения. При этом матрицы сходства и различия по определению соответствующих мер обладают свойством симметрии относительно главной диагонали, а матрицы мер включения таким свойством не обладают.

Отношения сходства, различия и включения, порождаемые соответствующими мерами, определяются следующим образом:

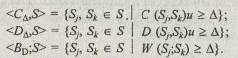
Здесь j, k Î J; С_D, D_D, B_D —соответственно отношения сходства, различия и включения; D— некоторое произвольное число (0£D £ 1,0 для отношения сходства и включения). Записи S_j С_D S_k и S_j B_D S_k означают соответственно то, что S_j и S_k находятся в отношении "D-сходства" и "D-банальности". Отношение "банальности" или "экзотичности" порождается мерой включения. При этом запись S_j B_D S_k означает, что описание S_j "банальнее" S_k при пороге D. Например, если рассчитанные для пары объектов меры включения имеют следующие значения: W(S₁; S₂) = 0,57, W(S₂; S₁)= 0,67, то эти результаты можно интерпретировать следующим образом. Мера включения первого описания во второе (0,67) показывает, что второй объект "оригинальнее", или "экзотичнее", первого. Т. e. описание второго объекта содержит больше специфических признаков, чем описание первого объекта, поскольку первое описание включено во второе на 67 %, а второе включено в первое на 57 %.

Отношение иерархии определяется следующим образом. Если множество H⁽ⁱ⁾ образовано соединением некоторых классов из множества Н⁽ⁱ⁾, то f: Н⁽ⁱ⁾ ® Н^(j) сюръективно: каждому элементу Н⁽ⁱ⁾ соответствует хотя бы один элемент из Н^(j). То обстоятельство, что класс появляется классом более широким, чем Н^(j) отображается через отношение иерархии И следующим образом: Н⁽ⁱ⁾ И Н^(j) (класс H⁽ⁱ⁾ подчиняет класс H^(j)).

Множество H⁽ⁱ⁾ называется сгущением H^(j), если хотя бы один из классов H⁽ⁱ⁾ есть соединение классов из H^(j).

Если И = {Н⁽¹⁾,..., H^(S)} есть множество разбиений, таких, что Н^(k) сгущение Н^(k-1), где k Î К, К = {k ½ k — целое число, 1 £ k £ S}, то в предельном случае Н⁽¹⁾ состоит из всех классов, содержащих ровно по одному элементу, a H^(S) — из одного класса, совпадающего с исходным множеством исследуемых объектов J. При этом если задано разбиение, то элементы, входящие в один и тот же класс, являются неразличимыми (эквивалентными). Здесь под разбиением Н множества J понимается представление J в виде совокупности непустых подмножеств H_k, k = 1, 2,..., п , таких, что

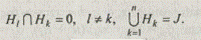
Множество И есть иерархическая система, состоящая из S уровней. Номеру каждого уровня можно поставить в соответствие его ранг, так как К— упорядоченное множество, а названия всех классов одного ранга считать категорией.

При практической реализации иерархических классификаций строятся дендрограммы, являющиеся графическим способом изображения системы, что делает наглядной структуру иерархической системы. Последовательный процесс построения сгущений начинается с рассмотрения q объектов {q Î H⁽¹⁾). Таким образом, на первом шаге каждый объект из заданного множества считается классом. Далее два наиболее схожих объекта объединяются в один класс, и общее число последних становится равным q -1. Эти классы принадлежат разбиению H⁽²⁾, являющемуся сгущением Н⁽¹⁾. Если число схожих объектов п, то объединяются любые два из них. Среди оставшихся снова отыскиваются наиболее схожие, которые также объединяются. Аналогичные процедуры осуществляются до тех пор, пока все объекты не попадут в один класс H^(S).

Одним из наиболее распространенных и простых подходов построения дендрограмм является подход, основанный на использовании матрицы сходства.

Определение сходства каждого вновь образованного класса со всеми остальными может производиться на основе матриц сходства шестью наиболее употребительными методами, которые описываются единой формулой:

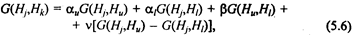
где G(H_j,H_k) — мера сходства или различия классов H_j и H_k = {Н_и ,H_l}.

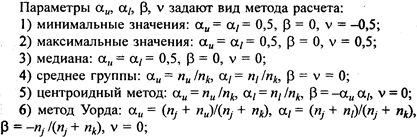
Здесь n_u, n_k — число объектов соответственно u-го и k-го классов; п_k = n_u + n_l.

Конкретный метод подбирается проектировщиком индивидуально для исследуемой предметной области с учетом ее специфики. Единых правил выбора не существует. Главным критерием для выбора метода классификации может являться хорошая интерпретируемость получаемых результатов, не противоречащих физическому смыслу изучаемой предметной области.