Метод нечеткого логического вывода в задаче выбора фирмой кандидата на замещение вакантной должности бухгалтера

Руководство фирмы рассматривает кандидатов на замещение вакантной должности бухгалтера. Задача заключается в том, чтобы, используя описанный выше метод, выявить наилучшего претендента. Обсуждение среди членов руководства фирмы дало следующий результат:

d₁: "Если кандидат имеет требуемые квалификацию, образование и опыт ведения бухгалтерского учета, то он — удовлетворяющий (отвечающий требованиям)";

d₂: "Если он вдобавок к вышеописанным требованиям умеет работать с современным программным обеспечением (ПО), то он — более чем удовлетворяющий";

d₃: "Если он дополнительно к условиям d₂ обладает необходимыми юридическими знаниями, то он — безупречный";

d₄: "Если он имеет все оговоренное в d₃, кроме способности работать с современным ПО, то он — очень удовлетворяющий";

d₅: "Если кандидат имеет необходимую квалификацию, имеет опыт ведения бухгалтерского учета, обладает юридическими знаниями, но не имеет высшего образования, он все же будет удовлетворяющим";

d₆: "Если он не имеет квалификации и не имеет опыта ведения бухгалтерского учета, то он — неудовлетворяющий".

Анализ приведенных информационных фрагментов позволяет выявить шесть критериев, используемых для принятия решения:

Х₁ — квалификация; Х₂ — образование; Х₃, — опыт ведения бухгалтерского учета; Х₄, — умение работать с современным ПО; Х₅ — юридическая грамотность, Y— удовлетворительность.

Для формулирования правил следует определить возможные значения лингвистических переменных X_i и Y, которые будут использоваться для оценки кандидатов:

d₁: "Если Х₁ = ПОДХОДЯЩЯЯ и X₂ = ВЫСШЕЕ, и Х₃ = ДОСТАТОЧНЫЙ. то Y = УДОВЛЕТВОРЯЮЩИЙ";

d₂: "Если Х₁ = ПОДХОДЯЩАЯ и X₂ = ВЫСШЕЕ, и Х₃ = ДОСТАТОЧНЫЙ, и X₄ = СПОСОБЕН, то Y = БОЛЕЕ ЧЕМ УДОВЛЕТВОРЯЮЩИЙ";

d₃: "Если Х₁ = ПОДХОДЯЩАЯ и Х₂ = ВЫСШЕЕ, и X₃ = ДОСТАТОЧНЫЙ, и Х₄ = СПОСОБЕН, и X₅ = ОБЛАДАЕТ, то Y = БЕЗУПРЕЧНЫЙ";

d₄: "Если Х₁ = ПОДХОДЯЩАЯ и Х₂ = ВЫСШЕЕ, и Х₃ = ДОСТАТОЧНЫЙ, и X₄ = ОБЛАДАЕТ, то Y = ОЧЕНЬ УДОВЛЕТВОРЯЮЩИЙ";

d₅: "Если Х₁ = ПОДХОДЯЩАЯ и X₂ = НЕ ВЫСШЕЕ, и Х₃ = ДОСТАТОЧНЫЙ, и X₅ = ОБЛАДАЕТ, то Y = УДОВЛЕТВОРЯЮЩИЙ";

d₆: "Если Х₁ = НЕ ИМЕЕТ и Х₃ = НЕДОСТАТОЧНЫЙ, то Y = НЕУДОВЛЕТВОРЯЮЩИЙ".

Переменная Y задана на множестве J = {0; 0,1; 0,2; ...; 1}.

Значения переменной Y заданы с помощью следующих функций принадлежности:

S = УДОВЛЕТВОРЯЮЩИЙ определено как m_S(х) = х, х Î J;

MS = БОЛЕЕ ЧЕМ УДОВЛЕТВОРЯЮЩИЙ —какm_MS(x)=Öx; x Î J;

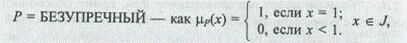
VS = ОЧЕНЬ УДОВЛЕТВОРЯЮЩИЙ — как m_VS(x) = х², x Î J,

US = НЕУДОВЛЕТВОРЯЮЩИЙ — как m_VS(x) = 1 - х, х Î J.

Выбор производится из пяти кандидатов на множестве U = {u₁, и₂, u₃, u₄, u₅}.

В рассматриваемой задаче оценки кандидатов заданы следующими нечеткими множествами:

ПОДХОДЯЩАЯ (квалификация) А = {0,8/u₁, 0,61u₂, 0,5/u₃, 0,1/u₄, 0,3/u₅};

ВЫСШЕЕ (образование) В = {0,5/u₁,1/u₂, 0/u₃, 0,5/u₄, 1/u₅};

ДОСТАТОЧНЫЙ (опыт) С = {0,6/u₁, 0,9/и₂, 1/u₃, 0,7/u₄, 1/u₅};

СПОСОБЕН (работать с ПО) D = {1/u₁, 0,3/и₂, 1/u₃, 0/u₄, 0/u₅}',

ОБЛАДАЕТ (юридическими знаниями) Е = {0/u₁, 0,5/u₂, 1/u₃, 0,8/u₄, 1/u₅}.

С учетом введенных обозначений правила d₁, ...,d₆ принимают вид:

d₁ : “Если Х= А и В, и С, то Y =S”;

d₂: "Если Х= А и В, и С, и D, то Y = MS":

d₃: “Если X= А и В, и С, и D, и E, то Y = P”;

d₄:“Если X = А и B, и С, и Е, то Y = VS”;

d₅: “Если X = A, и не В, и С, и E, то Y = S”;

d₆: “Если Х = не A и не С, то Y = US”.

Вычислим функции принадлежности 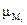длялевых частей приведенных правил:

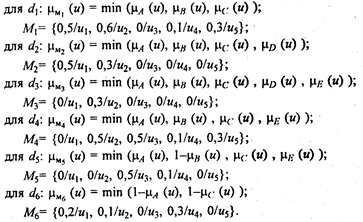
Теперь правила можно записать в виде:

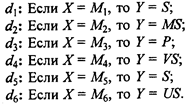
Используя для преобразования правил вида "Если Х = М, то Y = Q" импликацию Лукасевича m_D(u, j) = min(l, 1-m_M /(u) + m_Y (j)), для каждой пары (u, j) Î U х J получаем следующие нечеткие отношения на U ´ J:

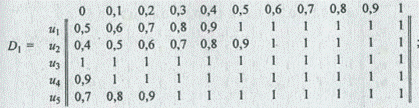
В результате пересечения отношений D₁, ..., D₆ получаем общее функциональное решение:

Для вычисления удовлетворительности каждой из альтернатив применим правило композиционного вывода в нечеткой среде:

E_k = G_k ° D, где Е_k — степень удовлетворения альтернативы k;

G_k — отображение альтернативы k в виде нечеткого подмножества на U, D — общее функциональное решение. Тогда

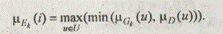
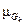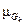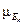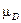Кроме того, в этом случае (u) =0; u ¹ u_k, (u) = 1; u = u_k. Отсюда (i) = (u_k, i) Другими словами, Е_k есть k-я строка в матрице D. Теперь применим описанную выше процедуру для сравнения нечетких подмножеств в единичном интервале для получения наилучшего решения на основе точечных оценок.

Для первой альтернативы

E₁ ={0,5/0; 0,6/0,1; 0,7/0,2; 0,8/0,3; 0,9/0,4; 1/0,5; 1/0,6; 1/0,7;1/0,8; 0,9/0,9; 0,8/1}.

Вычисляем уровневые множества E_ja и мощность такого множества М(Е_a) по формуле

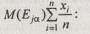
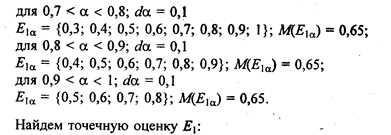
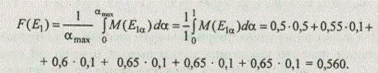
Аналогично находим точечные оценки длядругих альтернатив:

для второй альтернативы F(E₂) = 0,656;

для третьей — F(E₃) = 0,575;

для четвертой — F(E₄) = 0,483;

для пятой — F(E₅) = 0,562.

В качестве лучшей выбираем альтернативу, имеющую наибольшую точечную оценку. В нашем примере это альтернатива и₂, следовательно, она и будет наилучшей. Второе место занимает альтернатива u₃; третье – u₅, четвертое – и₁, а самой худшей из альтернатив является u₄.

Формализация знаний с помощью правил позволяет учитывать различную важность критериев и самих правил. Предположим, что в рассмотренной задаче ЛПР считает крайне важным умение кандидата на должность бухгалтера работать с программным обеспечением. Тогда в правилах d₂ и d₃ значением критерия Х₄ будет понятие ОЧЕНЬ СПОСОБЕН, описываемое нечетким множеством D₁ следующего вида:

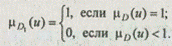
Правило d₄ исключим из рассмотрения, так как теперь кандидат, не владеющий умением работать с ПО, не является ОЧЕНЬ УДОВЛЕТВОРЯЮЩИМ. Тогда соответствующие левым частям правил нечеткие множества М_i, i = 1, .... 6, i ¹ 4, будут иметь вид:

F(u₁)—0,560; F(u₂)— 0,600; F(u₃)—0,575; F(u₄)— 0,475; F(u₅)— 0,530.

Сравнение полученных результатов показывает, что с повышением значимости критерия Х₄ ранжировка альтернатив несколько изменилась: и₁ и u₅ поменялись местами. Этот факт согласуется с исходными данными, так как кандидат и₁ имеет максимальное значение по критерию Х₄, а u₅ - минимальное.

Для учета различной важности правил будем использовать нормированные весовые коэффициенты, которые можно получить либо путем попарных сравнений, либо путем экспертного назначения весов.

В рассматриваемой задаче возможны различные подходы к выбору кандидата на должность: мягкий, жесткий, рациональный и т. д. Мягкий подход обычно имеет место в условиях дефицита времени и квалифицированных кадров, основную директиву этого подхода можно сформулировать так: "лишь бы умел что-нибудь делать". При мягком подходе самый большой вес будет иметь правило d₆ а все остальные будут одинаково значимыми. Значения весовых коэффициентов правил приведены в табл. 4.5.

Жесткий подход к выбору кандидата на должность возможен в случае избытка квалифицированных кадров и ресурса времени, отводимого для выбора. Целью такого подхода является поиск кандидата, наиболее соответствующего идеалу. Назначенные ЛПР экспертные оценки важности правил с использованием 10-балльной шкалы и соответствующие весовые коэффициенты приведены в табл. 4.5.

Таблица 4.5