Нечеткие операции, отношения и свойства отношений
Операции над нечеткими множествами. Над нечеткими множествами, как и над обычными, можно выполнять математические операции. Рассмотрим важнейшие из них: дополнение множества, объединение и пересечение множеств.
Операция дополнения может быть представлена следующим образом:
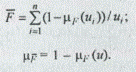
Операция объединения будет иметь следующий вид:
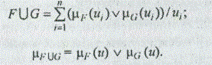
Здесь и далее операция v обозначает взятие максимума. Операция пересечения вычисляется следующим образом:
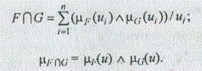
Здесь и далее символ л обозначает взятие минимума.
Нечеткие отношения. Нечетким отношением R между полным множеством U и другим полным множеством V называется подмножество прямого декартова произведения U ´ V, определяемое следующим образом:
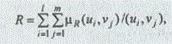
где U = {u1, u2,..., иl}, V {v1, v2,..., vm}.
Допустим, что между элементами знаний, представленных нечеткими множествами F и G, существует связь, заданная правилом: "Если F, то G", при этом F Í U, G Í V. В логике высказываний для представления правил подобного вида используется операция импликации. В нечеткой логике предложены различные способы реализации импликации. Один из наиболее простых способов заключается в представлении импликации, соответствующей правилу "Если F, то G", нечетким отношением R, которое вычисляется следующим образом [2]:
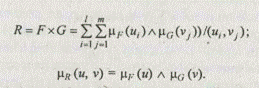
Дата добавления: 2021-01-11; просмотров: 505;











