Сложение и умножение целых чисел.

Определим на множестве целых чисел действия сложения и умножения по следующим правилам:

.

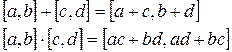Теорема 2. Действия сложения и умножения целых чисел являются бинарными операциями на фактормножестве .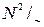

Доказательство.

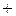- бинарная операция (?)

Сложение определено 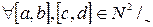, т.к. определено сложение любых натуральных чисел. Покажем однозначность.

.

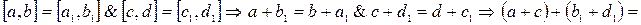
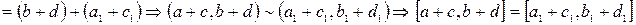- бинарная операция (?)

Умножение определено 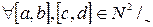, т.к. определено сложение и умножение любых натуральных чисел. Покажем однозначность.

.

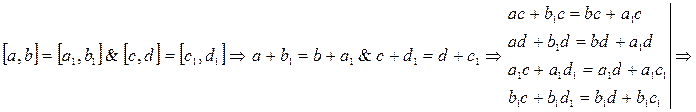
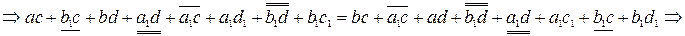
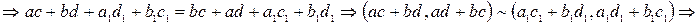
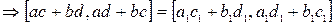Поскольку 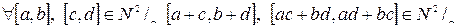в силу того, что сумма и произведение натуральных чисел также являются натуральными числами, множество 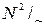замкнуто относительно сложения и умножения.

что и требовалось доказать.

Кольцо целых чисел.

Теорема 3. 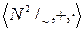- целостное кольцо, т.е. коммутативное кольцо с единицей, не содержащее делителей нуля.

Доказательство.

Проверим аксиомы кольца.

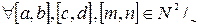
1) 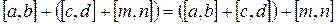(ассоциативность +) (?)

.

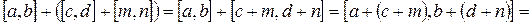
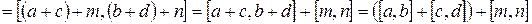2) 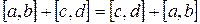(коммутативность +) (?)

.

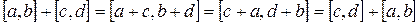3) 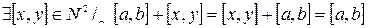(существование 0) (?)

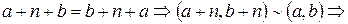
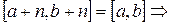
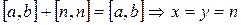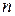, где - произвольное натуральное число.

4) 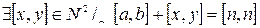(существование противоположного) (?)

.

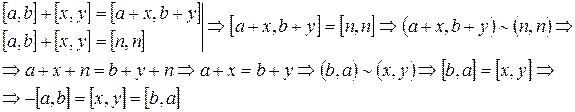5) 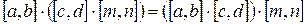(ассоциативность ) (?)

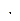6) 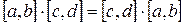(коммутативность ) (?)

.

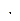7) 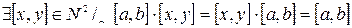(существование 1) (?)

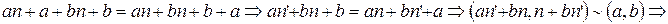
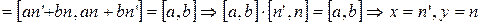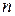, где - произвольное натуральное число.

8) 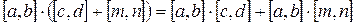(дистрибутивность) (?)

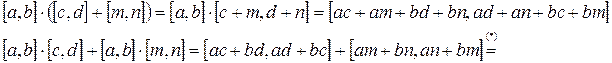
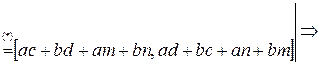
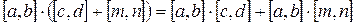
9) 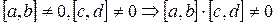(отсутствие делителей 0) (?)

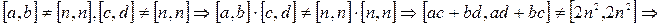
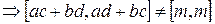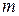, где - произвольное натуральное число, в силу произвольности 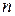. Таким образом, .

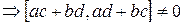что и требовалось доказать.