Описание лабораторной установки
Схема экспериментальной установки для исследования электрической цепи с последовательным соединением элементов R, L, C представлена на рис.4.8.
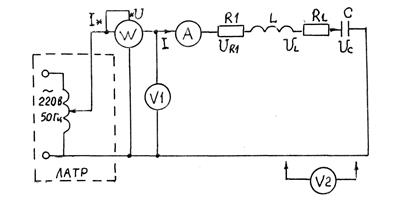
Рис.4.8.
В её состав входят ЛАТР (лабораторный автотрансформатор), на выходных клеммах которого устанавливается напряжение U = 40 В.
Вольтметр V1 предназначен для измерения действующего значения напряжения, прикладываемого к электрической цепи; соответственно измеряет действующие значения напряжения на элементах R, L, C.
Амперметр А измеряет действующее значение тока в цепи. В качестве R1 используется реостат (Rреост = 30 Ом, 5 А), емкости С – магазин емкостей (С = 1 мкФ ÷ 20 мкФ), индуктивности L – катушка индуктивности (с параметрами L и RL, определяемыми экспериментально).
Лабораторная работа. Параллельное соединение элементов R, L, C
Цель работы – исследование электрической цепи с параллельным соединением элементов R, L, C при различных соотношениях индуктивного и емкостного сопротивлений.
Общие сведения
При параллельном соединении элементов R, L, C (рис.4.9.) полная проводимость равна 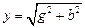 (4.19)
(4.19)
где g = 1/R – активная проводимость цепи;
b – реактивная проводимость цепи.
Реактивная проводимость цепи при этом определяется выражением
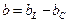 (4.20)
(4.20)
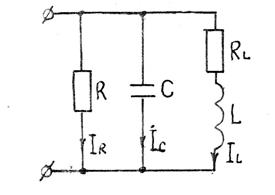
Рис. 4.9.
Ток в цепи определяется выражением
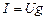 (4.21)
(4.21)
Ток в активной проводимости совпадает с напряжением по фазе
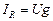 (4.22)
(4.22)
Ток в ёмкости определяет напряжение по фазе на 900
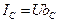 (4.23)
(4.23)
Ток в индуктивности отстаёт от напряжения по фазе на 900
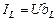 (4.24)
(4.24)
Средняя активность мощность, расходуемая в цепи
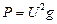 (4.25)
(4.25)
Сдвиг фаз между напряжением U на зажимах цепи и током I в ней определяется выражениями
 (4.26)
(4.26)
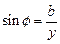 (4.27)
(4.27)
Векторная диаграмма напряжения и токов в цепи показана на рис.4.10. (при bC > bL).

Рис.4.10.
Резонансом токов называется такое состояние электрической цепи при параллельном включении элементов R, L, C, когда сдвиг по фазе между напряжением на зажимах цепи и током в ней равны нулю, при этом bC = bL, а ток в неразветвлённой цепи имеет наименьшее значение.
При постоянных значениях L и C резонансная частота определяется выражением
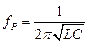 (4.28)
(4.28)
Резонансное значение тока в цепи
 (4.29)
(4.29)
Ток в активной проводимости при резонансе равен полному току
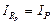 (4.30)
(4.30)
Токи в ёмкости и индуктивности при резонансе равны между собой
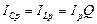 (4.31)
(4.31)
где 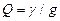 - добротность контура;
- добротность контура;
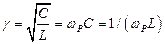 - волновая и характеристическая проводимость контура.
- волновая и характеристическая проводимость контура.
Средняя мощность при резонансе
 (4.32)
(4.32)
Векторная диаграмма напряжения и токов при резонансе токов показана на рис.4.11.
Настроить цепь в резонанс с частотой источника питания можно изменением индуктивности или ёмкости, а также с помощью изменения частоты источника питания.
Графики изменений токов цепи, сдвига фаз и напряжения на зажимах цепи при изменении частоты источника питания называются частотными характеристиками контура и показаны на рис.4.12.
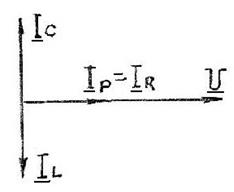
Рис.4.11.
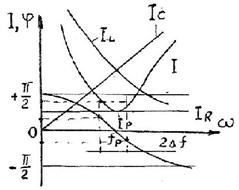
Рис.4.12.
Частотные характеристики контура могут быть построены по уравнениям (4.21), (4.22), (4.23), (4.26), (4.27).
Частотная характеристика тока позволяет определить экспериментально добротность контура
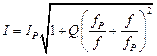 (4.33)
(4.33)
Если определить полосу пропускания частот  , пропускаемых контуром на уровне
, пропускаемых контуром на уровне 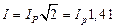 , то добротность контура можно найти из выражения
, то добротность контура можно найти из выражения
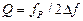 (4.34)
(4.34)
На границе полосы пропускания сдвиг фаз между напряжением на зажимах цепи и током в ней составляет φ = ± 450. Если катушка индуктивности L имеет собственное активное сопротивление (рис.4.13.), то ток в ней определяется выражением
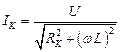 (4.35)
(4.35)
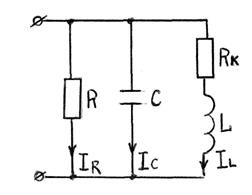
Рис.4.13.
Вычислив эквивалентные проводимости катушки
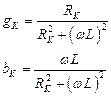 (4.36)
(4.36)
перейдём к эквивалентной схеме с параллельным соединением R, L, C.
Полная активная проводимость эквивалентного параллельного контура равна сумме внешней проводимости 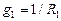 и собственной активной проводимости gK катушки L
и собственной активной проводимости gK катушки L
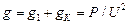 (4.37)
(4.37)
Эквивалентная индуктивность такого контура
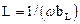 (4.38)
(4.38)
Резонансная частота контура будет зависеть от собственного сопротивления RK катушки L
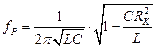 (4.39)
(4.39)
При относительно малом сопротивлении катушки RK >> ωL можно пользоваться выражениями (4.28 ÷ 4.34).
Содержание работы
Исследование электрической цепи с параллельным соединением резистора, катушки индуктивности и конденсатора при различных соотношениях индуктивного и ёмкостного сопротивлений.
Дата добавления: 2016-09-26; просмотров: 1969;











