Сарос. История затмений.

Последовательность затмений повторяется почти точно в прежнем порядке через промежуток времени, который называется саросом. Сарос (египт. - повторение) был вычислен ещё в древности и составляет 18 лет и 11,3 суток.

В течение каждого сароса происходит 70 затмений, из них 41 солнечное и 29 лунных. Солнечные затмения происходят чаще лунных, но в данной точке на поверхности Земли чаще можно наблюдать лунные затмения, так как они видны на целом полушарии Земли, тогда как солнечные затмения видны лишь на узкой полосе. Полных солнечных затмений в течение сароса бывает 10, но их редко можно увидеть. В данной точке Земли солнечные затмения видны в среднем 1 раз в 200 - 300 лет.

По древней китайской легенде придворные астрономы Хи и Хо, жившие в XXII в. до н. э., предались пьянству и не предсказали вовремя солнечное затмение 22 октября 2137 г. до н.э. Затмение наступило во время торжественной церемонии, нарушив её ритуал. Астрономам отрубили головы.

Сарос был открыт вавилонянами не позднее 6 в до н.э. Клавдий Птолемей описал его в Альмагесте со ссылкой на вавилонских астрономов:

"Древнейшие математики нашли из наблюдений лунных затмений, что за промежуток в 6585 1/3 дня заканчивается приблизительно 223 синодических месяца, 239 аномалистических, 242 возвращения по широте (драконических), 241 возвращение по долготе (сидерических) и сверх того 10 2/3 градусов, которые Солнце прошло за то же время сверх своих 18 оборотов, считая их по отношению к неподвижным звёздам; и они называли этот промежуток времени периодом, так как после него все эти движения возвращаются к исходному положению."

В 19 веке были найдены клинописные таблички древнего Вавилона. На одной из них есть таблица саросов с -372 до -276 г. .

Авторами теории затмений в Вавилоне были астрономы Кидинну и Набу-риманну.

Сообщения о затмениях в Вавилоне носили такой характер: "Четырнадцатого произойдёт затмение; это - неблагоприятно для Элама и Амурру, но благоприятно для царя, мой господин; пусть царь, мой господин, успокоится. Оно будет видно без Венеры. Из Ирасшиилу, царский слуга."

Начала небесной механики.

Законы Кеплера.

Иоганн Кеплер родился в 1571 году. Закончил Тюбингенскую духовную академию. После окончания занимался преподаванием.

Книга "Предвестник космографических изысканий, содержащий космографическую тайну об удивительном соотношении небесных сфер, а также истинные и должные причины числа небес, их величин и периодических их движений, объяснённую посредством пяти правильных геометрических тел" показала большие математические способности и послужила сближению Кеплера с Тихо Браге. В дальнейшем И. Кеплер вывел свои законы на основании наблюдений, собранных Тихо Браге.

В 1609 году вышла в свет книга "Новая астрономия, причинно обоснованная, или физика неба, изложенная в исследованиях движения звезды Mарс, по наблюдениям благороднейшего мужа Тихо Браге". В этой книге формулировались первые два закона движения небесных тел. Третий закон появился спустя 10 лет исследований в книге "Гармония мира", вышедшей в 1619 году. Долгие годы исследований заставили Кеплера отречься от прежних идеализированных воззрений на природу движения небесных тел.

Законы Кеплера формулируются следующим образом:

1. Все планеты движутся по эллипсам, в одном из фокусов которых (общем для всех планет) находится Солнце.

2. Радиус - вектор планеты в равные промежутки времени описывает равновеликие площади.

3. Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит.

,

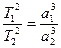где Т₁, Т₂ - сидерические периоды обращений планет, а₁, а₂ - большие полуоси их орбит. Если большие полуоси орбит выражать в единицах среднего расстояния от Земли до Солнца (в а.е.), а периоды обращений в годах, то для Земли а = 1, Т = 1, и период обращения любой планеты вокруг Солнца равен:

.

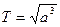Если обобщить законы Кеплера на различные случаи движения небесных тел, получим следующие формулировки:

1. Под действием силы притяжения одно небесное тело движется в поле тяготения другого небесного тела по одному из конических сечений - кругу, эллипсу, параболе или гиперболе.

2. Площадь, описанная радиусом вектором за единицу времени есть величина постоянная.

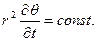
где r – радиус-вектор, q - полярный угол (истинная аномалия).

3. ,

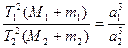где M₁ и M₂ – массы главных тел, а m₁ и m₂ – массы спутников, a1 и a2 – большие полуоси орбит спутников.