Прецессия и нутация земной оси.

Вследствие возмущающего действия, оказываемого на вращение Земли телами Солнечной системы, ось вращения Земли совершает в пространстве очень сложное движение. Земля имеет форму сфероида, и поэтому различные части сфероида притягиваются Солнцем и Луной неравномерно.

1. Ось медленно описывает конус, оставаясь всё время наклонённой к плоскости движения Земли под углом около 660,5. Это движение называется прецессионным, период его около 26 000 лет. Оно определяет среднее направление оси в пространстве в различные эпохи.

2. Ось вращения Земли совершает различные мелкие колебания около своего среднего положения, главные из которых имеют период 18.6 года, (этот период есть период обращения узлов лунной орбиты, так как нутация есть следствие действия притяжения Луны на Землю) и называются нутацией земной оси. Нутационные колебания возникают, потому что прецессионные силы Солнца и Луны непрерывно меняют свою величину и направление. Они = 0, когда Солнце и Луна находятся в плоскости экватора Земли и достигают максимума при наибольшем удалении от него.

Вследствие прецессии и нутации взаимное расположение полюсов мира и полюсов эклиптики непрерывно изменяется.

3. Притяжение планет мало, чтобы вызывать изменения положений земной оси. Но планеты влияют на положение земной орбиты. Изменения положений плоскости эклиптики под воздействием притяжения планет называется планетной прецессией.

Полюс мира, определяемый средним направлением оси вращения Земли, т.е. обладающий только прецессионным движением, называется средним полюсом мира.

Истинный полюс мира учитывает и нутационные движения оси.

Средний полюс мира вследствие прецессии за 26 000 лет описывает около полюса эклиптики окружность радиусом 230,5. За один год перемещение среднего полюса мира на небесной сфере составляет около 50",3. На такую же величину перемещаются на запад и равноденственные точки, двигаясь навстречу видимому годовому движению Солнца. Это явление называется прецессией или предварением равноденствий. Вследствие этого Солнце попадает в равноденственные точки раньше, чем на то же самое место на фоне звёзд. Полюс мира описывает незамыкающийся круг на небесной сфере. 2000 лет до н.э. полярной звездой была a Дракона, через 12 000 лет полярной станет a Лиры.

В начале нашей эры точка весеннего равноденствия находилась в созвездии Овна, а точка осеннего равноденствия в созвездии Весов. Сейчас точка весеннего равноденствия находится в созвездии Рыб, а осеннего в созвездии Девы.

Прецессионное движение полюса мира вызывает изменение координат звёзд с течением времени.

Влияние прецессии на координаты:

da/dt = m + n sin a tg d,

dd/dt = n sin a.

где da/dt, dd/dt - изменения координат за год, m - годичная прецессия по прямому восхождению, n - годичная прецессия по склонению.

Из-за непрерывного изменения экваториальных координат звёзд, происходит медленное изменение вида звёздного неба для данного места на Земле. Некоторые невидимые ранее звёзды будут восходить и заходить, а некоторые видимые - станут невосходящими. Так, через несколько тысяч лет в Европе можно будет наблюдать Южный Крест, но нельзя будет увидеть Сириус и часть созвездия Ориона.

Истинный полюс мира описывает вокруг среднего полюса сложную кривую. Его движение на небесной сфере совершается приблизительно по эллипсу, большая полуось которого равна 18",4, а малая 13",7. Он совершает один оборот за 18,6 года. Это движение истинного полюса мира вокруг среднего называется нутацией.

Прецессия была открыта Гиппархом и объяснена И. Ньютоном.

Задача трёх тел.

Определение движения трёх тел, взаимно притягивающих друг друга с силой, обратно пропорциональной квадрату расстояния между ними, называется задачей трёх тел.

Эта задача очень сложна и её математическое решение трудно. В 1912 году финский математик К. Зундман нашёл формальное решение этой задачи. Он выразил результат в виде степенных рядов. Однако, для расчётов солнечных затмений в рядах Зундмана нужно удерживать число членов, равное примерно единице с 40 нулями.

Лагранж в 1772 году доказал, что существует определённое количество частных случаев в этой задаче, для которых может быть найдено точное решение.

Рассмотрим два из них. В обоих случаях тела описывают подобные между собой кеплеровские орбиты с фокусами в центре масс.

1. Тела образуют лагранжеву конфигурацию - равносторонний треугольник, который может пульсировать в своих размерах и вращаться в своей плоскости в постоянном направлении.

2. Тела образуют эйлерову конфигурацию и находятся на прямой, проходящей через центр масс, и оставаясь на ней, вращаются и пульсируют аналогичным образом. Этот случай был найден Л.Эйлером независимо от Лагранжа в 1767 году.

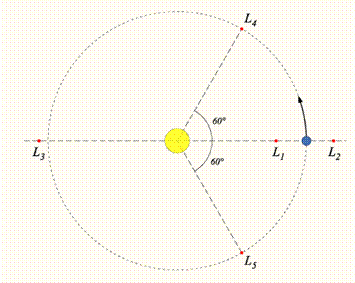Если заданы массы тел и их положение на плоскости, то рассматриваемые частные случаи движения в этой плоскости получаются при рассмотрении третьего тела в одной из пяти точек, называемых точками либрации или точками Лагранжа.

Первые три точки либрации располагаются в определённых точках прямой, соединяющей обе заданные массы, причём одна между ними, а две другие - вне их. Четвёртая и пятая точки являются вершинами двух равносторонних треугольников, в которых остальные вершины заняты заданными массами.

Лагранж показал, что если третье тело находится в одной из пяти точек либрации, то конфигурация, которую образуют все три тела, всегда остаётся подобной самой себе, а их движение происходит по коническим сечениям одинакового вида.

1. Если тела находятся на одной прямой, то они обращаются, оставаясь на ней, вокруг общего центра масс.

2. Если три тела расположены в вершинах равностороннего треугольника, то они обращаются вокруг общего центра масс так, что треугольник остаётся всё время равносторонним.

В начале ХХ века были открыты две группы астероидов, движение которых соответствует второму решению Лагранжа. В 1907 году был открыт 588 Ахиллес, позднее ещё восемь “греков”, движущихся по соседству с Ахиллесом. Пять “троянцев” движутся с другой стороны. Эти астероиды находятся в точках либрации системы Солнце - Юпитер.

В системе Земля-Луна тоже существуют точки либрации. Эйлеровы называются коллинеарными, а лагранжевы - эквидистантными.

Точки либрации могут быть устойчивыми, лишь когда отношение масс больших тел достаточно мало.

Прямолинейные точки неустойчивы. Достаточно малой возмущающей силы, чтобы либроид удалился из окрестности данной точки. Треугольные точки будут устойчивыми почти для всех достаточно малых отношений масс. Неустойчивость может быть только в двух случаях, когда отношение масс равно одному из двух чисел - 0,0137 и 0,0249.

В 1961 году польский астроном К. Кордылевский наблюдал облакообразные скопления в треугольных точках системы Земля-Луна.

Точки либрации используются в космонавтике.

Задача n тел.

Задача определения четырёх и более тел (задача n тел), притягивающих друг друга по закону Ньютона, ещё более сложна, чем задача трёх тел и в общем виде до сих пор не решена.

Задача N тел в общем виде формулируется следующим образом: “В пустом пространстве помещено N свободных материальных точек, которые притягиваются друг к другу по закону Ньютона. Заданы их начальные координаты и начальные скорости. Определить последующее движение этих точек”.

Решение задачи одного тела даёт 1-й закон Ньютона: “Всякое тело удерживается в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не побуждается приложенными силами изменить это своё состояние”.

Задача двух тел тоже была решена И. Ньютоном и рассмотрена нами выше.

Для исследования движений n тел применяется метод вычисления возмущений, позволяющий найти приближённое решение задачи. Сейчас существует целый ряд методов для приближённого решения задачи, позволяющих для каждой конкретной системы тел с заданными конкретными начальными условиями построить траектории движения с любой нужной для практики точностью для любого ограниченного отрезка времени.

На ЭВМ было промоделировано движение пяти внешних планет Солнечной системы за 400 лет - с 1653 по 2060 год. Результаты вычислений совпали с данными наблюдений.

Однако конкретные численные методы не могут дать ответы на многие вопросы качественного характера, например:

- Будет ли одно из тел всегда оставаться в некоторой области пространства или сможет удалиться в бесконечность?

- Может ли расстояние между какими-либо двумя из этих тел неограниченно убывать, или, напротив, это расстояние будет заключено в определённых пределах?

- Распадётся ли когда-нибудь Солнечная система, если считать, что она состоит из тел, движение которых возмущается малыми силами со стороны всех остальных небесных тел?

Пьер Симон Лаплас в 1799 - 1825 гг. решал задачу о движении планет и их спутников под действием силы тяготения Солнца и их взаимного гравитационного воздействия. Лаплас учёл движения 18 тел. Он считал, что точное движение планет временами нарушается и необходимо внешнее вмешательство, чтобы восстановить порядок.

В.И. Арнольд доказал несколько теорем, по которым следует, что Солнечная система не распадётся ещё многие миллионы лет.

8.8 Открытие новых планет.

В 1781 году Вильям Гершель открыл новую большую планету Уран, которую раньше принимали за звезду. К 1840 году стало ясно, что орбита Урана отличается от предсказанной по теории Ньютона. В орбите были заметны отклонения от теоретически вычисленной траектории.

Было сделано предположение, что, движение Урана возмущает какое-то массивное тело, находящееся за его орбитой.

Ж.Ж. Леверье и Дж.К. Адамс независимо друг от друга вычислили положение этого тела. Адамс дал свои вычисления в Гринвичскую и Кембриджскую обсерватории, но на них не обратили должного внимания.

Леверье сообщил о своём открытии в Берлинскую обсерваторию Иоганну Готфриду Галле. Он сразу начал поиски объекта и обнаружил его на расстоянии 10от вычисленного. Это оказалась планета Нептун.

В 80-х годах нашего столетия на ЭВМ было промоделировано движение пяти внешних планет Солнечной системы за 400 лет - с 1653 по 2060 год. Результаты показали, что за орбитой Плутона нет никакой планеты, заметно возмущающей орбиты уже известных планет. Однако, сам Плутон почти не влияет на орбиту Нептуна из-за своей малой массы. Если за орбитой Плутона находятся такие же маломассивные планеты, то их почти невозможно обнаружить. Однако, проведённый эксперимент, очевидно, доказывает, что нет звезды - гипотетической Немезиды, входящей как второй звёздный компонент в Солнечную систему.