Решение размерной цепи методом неполной взаимозаменяемости (теоретико-вероятностным методом)
При методе максимума-минимума возможно сочетание наибольших увеличивающих звеньев и наименьших уменьшающих звеньев и обратные их сочетания. Такие сочетания маловероятны, т.к. наибольшую вероятность получения имеют размеры в середине поля допуска. Если допустить малую вероятность несоблюдения размеров в пределах допуска, то можно значительно расширить допускисоставляющих размеров, т.е. уменьшить себестоимость изготовления деталей.
Сущность метода: при расчете размерной цепи теоретико-вероятностным методом точность замыкающего звена обеспечивается не у всех изделий, а только у заранее обусловленной их части.
Метод основан на том, что при решении учитываются не предельные значения размеров, а вероятность их сочетания.
Количество изделий, у которых возможно необеспечение точности замыкающего звена (брак) называется процентом риска р (1%, 0,12%, 0,27%, 0,01%).
Например, при р = 0,27% у трех размерных цепей из тысячи не обеспечится допуск замыкающего звена А∆ в заданном интервале.
Уравнение размерной цепи в номиналах:
A∆ = Σ Aі ув. - Σ Aі ум. (1)
Допуск замыкающего звена:
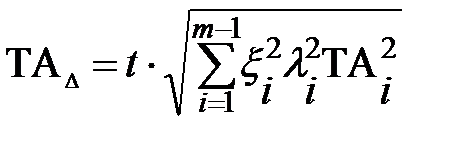 , (2)
, (2)
где t – коэффициент риска, зависит от процента брака р (выбирается по таблице).
Аi – номинальное значение составляющих звеньев;
ξi – передаточное отношение i – го звена разменной цепи (в линейных размерных цепях для увеличивающих звеньев ξ = +1, для уменьшающих звеньев ξ = -1);
m – общее число звеньев размерной цепи;
λ2і – коэффициент, учитывающий закон рассеяния размеров (при нормальном законе распределения размеров коэффициент λ2i = 1/9, если закон неизвестен, например, при изготовлении малых партий изделий, то λ2i = 1/3. Если распределение размеров подчиняется закону треугольника, то λ2i = 1/6.)
Средний допуск составляющих звеньев:
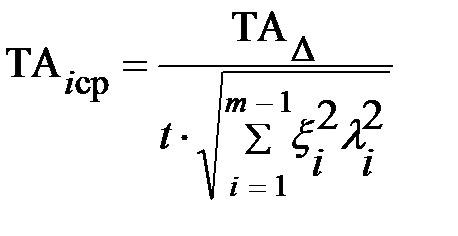 , (3)
, (3)
Метод применяется для расчета размерных цепей с количеством звеньев не менее 6-ти.
Последовательность решения задачи методом теоретико-вероятностным такая же как при методе максимума и минимума. Проверка производится по следующим зависимостям
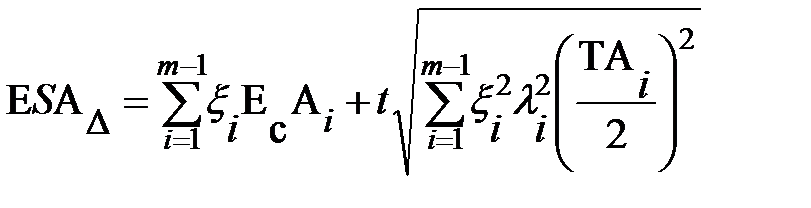 ;
;
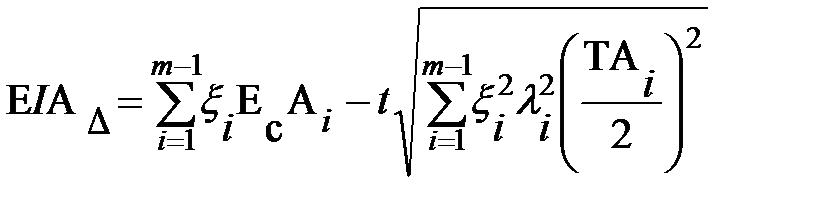 .
.
Дата добавления: 2016-09-26; просмотров: 2650;











