Динамика материальной точки и твердого тела. Законы Ньютона. Масса. Виды сил в механике: силы трения, трение покоя, скольжения и качения, силы упругости.

ЛЕКЦИЯ-2

Раздел механики, изучающий движение материальных тел совместно с физическими причинами, вызывающими это движение, называется динамикой.

В основе динамики лежат три закона Ньютона, сформулированные им в 1687 г. законы Ньютона играют исключительную роль в механике и являются обобщением результатов огромного человеческого опыта.

Первый закон Ньютона касается движения тел, не испытывающих внешних воздействий: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Таким образом, наличие скорости само по себе не показывает, действуют ли на тело внешние силы или нет; изменение скорости есть результат действия силы.

Как указывалось ранее, движение происходит всегда относительно некоторой системы отсчета. Закон Ньютона справедлив только для систем, движущихся без ускорения и называемых инерциальными системами. Первый закон Ньютона называют также законом инерции, так как оно связано с инертностью тел. Первый закон Ньютона говорит о существование инерциальных систем отсчета. Опыт показывает, что инерциальной можно считать гелиоцентрическую (звездную) систему отсчета – начало координат находится в центре Солнца, а оси проведены в направлении определенных звезд. Система отсчета, связанная с Землей, строго говоря, неинерциальна, однако при решении многих задач эффекты, обусловленные ее неинерциальностью пренебрежимо малы, поэтому ее считают инерциальной.

Опыт показывает, что при одинаковых воздействиях различные тела неодинаково изменяют скорость своего движения, то есть приобретают различные ускорения. Ускорение зависит не только от величины воздействия, но от свойств самого тела, то есть от его массы. Масса является одной из основных физических величин. Существенно, что она характеризует не только инерционные свойства тел, но и их гравитационные свойства. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10^-12 их значения). Чтобы описывать воздействия, вводят понятие силы. Под действием сил тела либо изменяют скорость движения, т.е. приобретают ускорение (динамическое проявление сил), либо деформируются (статическое проявление сил). В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения.

Второй закон Ньютонаустанавливает связь между изменением движения и внешними воздействиями, которым подвергается рассматриваемое тело. Изменение скорости движения данного тела пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует. При одной и той же силе ускорения различных тел неодинаковы, они зависят от массы тел. Учитывая, что сила и ускорение – величины векторные, можем записать

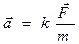(1)

Соотношение (1) выражает второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).

В Си коэффициент пропорциональности k=1. Тогда

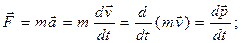(2)

Выражение (2) – более общая формулировка II закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе.

Векторная величина 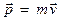называется импульсом (количеством движения) этой материальной точки.

Единица силы в СИ – ньютон (Н): .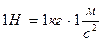

Обратим внимание на то, что: II закон Ньютона справедлив только в инерциальных системах отсчета; I закон можно сформулировать из II закона Ньютона.

Если на материальную точку действуют две силы, то их действие эквивалентно действию одной силы: 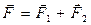, получаемого из треугольника сил. При увеличении количества сил правило остается то же, но получают векторный многоугольник, где замыкающая сила является равнодействующей. В механике большое значение имеет принцип независимости действия сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, равное произведению этой силы на массу точки. Согласно этому принципу, силы и ускорения можно разлагать на составляющие, что упрощает решение задач. Например, на рис.1 сила разложена на два компонента: тангенциальную силу 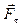(направлена по касательной к траектории) и нормальную силу 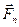(по нормали к центру).

Тогда можно записать:

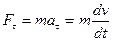и .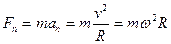

Третий закон Ньютона.Влияние на тело (материальную точку) не может односторонним, взаимодействие должно быть, по сути дела, обоюдным. Этот факт отражается третьим законом динамики, сформулированным для случая взаимодействия двух материальных точек (рис.2):

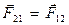. (3)

Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.

Применяя формулу импульса и второго закона Ньютона, можно записать:

;

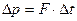где 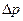– изменение импульса; 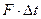– импульс действующей силы. Если на тело, или систему тел, не действует сила, то изменение импульса будет равна нулю. Это означает, что импульс данной системы не изменяется со временем. Последнее является выражением закона сохранения импульса замкнутой системы.

2. Динамика поступательного движения твердого тела. Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых может рассматриваться как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек,которая рассматривается как механическая система.

Механика рассматривает абсолютно твердые тела. Если мы имеем механическую систему, состоящую из многих тел, то согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направлены.

Закон сохранения импульса. Центр масс. Рассмотрим механическую систему, состоящую из nтел, масса и скорость которых соответственно равны m₁, m₂, …, m_n и 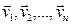. Пусть 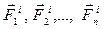– равнодействующие внутренних сил, действующих на каждое из этих тел, а 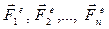– равнодействующие внешних сил. По II-закону Ньютона для каждого из nтел механической системы можно записать:

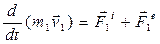
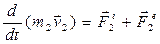(1)

. . . . . . . . . . .

.

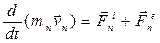Сложим почленно уравнения (1) и получим:

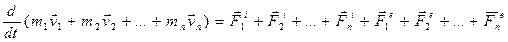. (2)

По III-закону Ньютона геометрическая сумма внутренних сил механической системы в выражении (2) равна нулю, тогда получим:

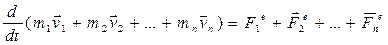. (3)

Здесь выражение в левой части равенства (3) является импульсом системы:

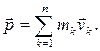(4)

Выражение (3) примет вид:

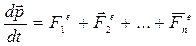, (5)

то есть, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему.

Если система замкнутая, то получим: ,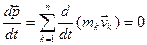

то есть: 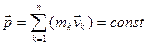, (6)

здесь n – число материальных точек в системе.

Выражение (6) является законом сохранения импульса: импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени. Этот закон справедлив не только в классической физике, но и в квантовой механике (для замкнутых систем микрочастиц. Поэтому этот закон носит универсальный характер – фундаментальный закон природы.

Закон сохранения импульса выражает свойство симметрии пространства – его однородность.

Так как масса не зависит от скорости движения, то импульс системы может быть выражен через скорость ее центра масс*, который определяется через радиус-вектор и скорость так:

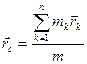и .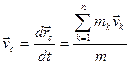

Учитывая выражение (4), можно записать

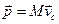, (7)

т.е. импульс системы равен произведению массы системы на скорость ее центра масс. Подставив выражение (7) в выражение (5), получим:

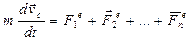, (8)

т.е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы. Выражение (8) представляет собой закон движения центра масс.

Уравнение движения тела переменной массы.Движение некоторых тел сопровождается изменением их массы. Например, масса ракеты изменяется за счет истечения газов, образующихся за счет сгорании топлива. Если в момент времени t масса ракеты m, а ее скорость v , по истечении времени dt ее масса уменьшится на dm, т.е. станет (m-dm), а скорость станет равной (v-dv). Изменение импульса системы за отрезок времени dt:

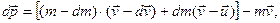
где 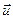– скорость истечения газов относительно ракеты. Тогда

.

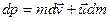Если на систему действуют внешние силы, то 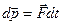, поэтому

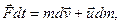
отсюда

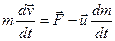. (9)

Величина 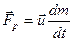называется реактивной силой. Нетрудно далее закончить рассуждения: если u противоположен v, то ракета ускоряется, если же совпадает с v, то тормозится.

Т.о. мы получим уравнение движения тела переменной массы:

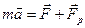, (10)

которое впервые было выведено И.В. Мещерским. Идея применения реактивной силы для создания летательных аппаратов высказывалась в ХIХ в. Н.И. Кибальчичем, К.Э.Циолковским.

Различные виды сил в механических процессахотличаются своим происхождением, зависимостью от координат, скоростей и т.п. например, силы тяготения, силы упругости и силы трения.

1. Силы трения: вызываются взаимодействием молекул соприкасающихся тел, направлены вдоль соприкасающихся поверхностей и зависят от их относительной скорости, направлены противоположно скорости движения. Различают внешнее (сухое) и внутреннее (вязкое) трение. В зависимости от состояния тела – покой или движение – говорят о трении покоя и о трении скольжения, трении качения. Последние относятся к сухому трению.

Рассмотрим лежащее на плоскости тело (рис.1), к которому приложена горизонтальная сила 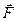. Если эта сила будет больше силы трения 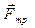, то тело придет в движение. Французские физики Г.Амонтон и Ш. Кулон опытным путем установили закон:

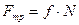
где f – коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей, которое можно определить с помощью рис.2.

Если тело находится на наклонной плоскости с углом наклона a, то оно приходит в движение только когда тангенциальная составляющая 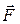силы тяжести 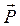больше силы трения 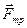. Следовательно, в предельном случае (начало скольжения тела)

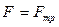или 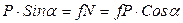, откуда .

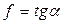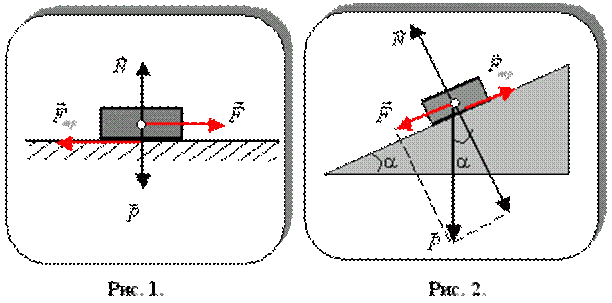
2. Радикальным способом уменьшения силы трения является замена трения скольжения трением качения (шариковые и роликовые подшипники). На рис. 3 изображено колесо, катящееся по горизонтальному участку пути.

Здесь движущая сила 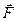образует пару с силой сцепления 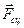колеса с поверхностью, момент которой будет зависеть от плеча r пары. Вес тела 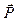и реакция поверхности 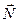образуют вторую пару с моментом, которая называется моментом трения качения 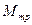, плечо этого момента d -является коэффициентом трения качения, зависит от степени деформации тела. А момент, образуемый парой сил 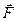и 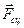называется движущим моментом 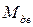. Если тело находится на наклонной плоскости с углом наклона a, то оно рассматривается аналогично тому, как мы уже рассмотрели для трения скольжения: катящееся тело приходит в движение только когда движущий момент будет больше момента трения качения.

3. В отличие от внешнего трения, во внутреннем трении отсутствует трение покоя. А если тела скользят относительно друг друга и разделены прослойкой вязкой среды – жидкости (смазки), то трение происходит в слое смазки. Это – гидродинамическое трение (если слой смазки достаточно толстый) или граничное трение (если толщина смазочной прослойки »0,1 мкм).

4.Силы упругости.Под воздействием тел друг на друга тела могут деформироваться, то есть одна его часть может смещаться относительно другой или изменится его форма. При этом внутри деформированного тела возникает противодействующая сила, называемая силой упругости или упругой силой.

Существует несколько видов деформации тел: односторонне растяжение, односторонне сжатие, всестороннее растяжение, всестороннее сжатие, кручение, сдвиг, изгиб. Каждый вид деформации вызывает появление соответствующей силы упругости.

Опыт показывает, что величина упругой силы, возникающей при малых деформациях любого вида, и смещения Dх (величины деформации) пропорциональны друг другу, т.е.

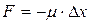
это соотношение называется законом Гука. Рассмотрим силы упругости, возникающей в деформированной пружине.

ЛЕКЦИЯ-3

Работа, энергия, мощность. Кинетическая и потенциальная, полная энергии. Сохранение полной энергии. Консервативная сила и потенциальная энергия. Соударение тел. Центр масс.

1. Энергия – это универсальная мера различных форм движения и взаимодействия. Каждой форме движения материи соответствует свои вид энергии: механическая, тепловая, электромагнитная, атомная, ядерная и др. В различных процессах один вид энергии может переходить в другой (другие) и наоборот, причем, энергия, отданная одним телом другому телу, равна энергии, полученной последним телом.

Изменение механического движения (энергии) тела вызывается силами, действующими на него со стороны других тел. Для количественной характеристики процесса обмена энергией между взаимодействующими телами в механике вводится понятие работы силы.Если на тело действует постоянная по направлению и значению сила 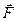, которая направлена под углом 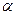к траектории движения, то работа определяется по формуле:

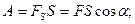(1)

В общем случае, когда сила переменная величина, весь участок пути, на котором определяется работа делят на элементарные участки, в пределах которого силу можно считать постоянной величиной и тогда элементарная работа определяется по формуле:

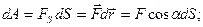(2)

Учитывая, что работа является величиной аддитивной, работу на всем участке пути можно определить:

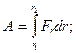(3)

Для характеристики быстроты совершения работы применяют величину – мощность:

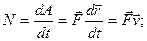(4)

Единица работы- джоуль(1Дж.=1Н м). Единица мощности- ватт (1Вт=!Дж/с).