Форми зображення чисел

У цифрових пристроях використовуються дві форми зображення чисел: з фіксованою і плаваючою комою.

У попередньому параграфі розглядались лише цілі позитивні числа. Формула (1.14) дає можливість зображати двійкові числа з цілою та дробовою частиною та з фіксованою комою. Знак двійкового числа з фіксованою комою задається допоміжним розрядом, який встановлюється перед числовими. Для додатних чисел значення допоміжного розряду рівне “0”, для від’ємних – “1”.

У табл. 1.3 приводяться три варіанти кодування додатних і від’ємних чисел чотирьохрозрядним двійковим кодом.

Taблиця 1.3.

У першому варіанті, як витікає з таблиці, у кодовій двійковій послідовності мають місце додатній і від’ємний нулі, що призводить до появи проблем при виконанні арифметичних операцій.

Представлення від’ємних чисел у зворотному коді також не вирішує відміченої проблеми. Вона вирішується лише тоді, коли від’ємні числа представляються у додатковому коді, який обчислюється за формулою:

.

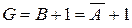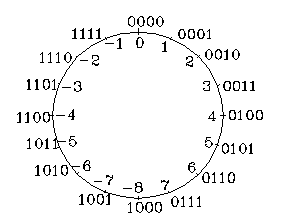
Рис.1.12.

На рис. 1.12 приведена графічна інтерпретація зображення позитивних і негативних чисел відносно нуля з використанням прямого та доповнюючого кодів. Як буде показано пізніше, така форма представлення десяткових чисел суттєво спрощує виконання арифметичних операцій.

Приклад 1.10. Знайти доповнюючі коди десятковим числам: 0₁₀, 17₁₀, -127₁₀.

Розв’язання. Знаходимо двійкові еквіваленти заданих чисел:

0₁₀ = 00000000₂ ; 17₁₀ = 00010001₂ ; -127₁₀ = 10000001₂ .

Знаходимо коди, зворотні двійковим – відповідно: 11111111; 11101110; 01111110.

Знаходимо доповнюючі коди заданих чисел: 11111111 + 1 = 100000000₂ = 0₁₀ ;

11101110 + 1 = 11101111₂ = -17₁₀ ; 01111110 + 1 = 01111111₂ = 127₁₀.

Тепер пояснимо суть запису чисел з фіксованою комою. Будь-яке число в цифрових системах зберігається спеціальними пристроями пам’яті, кожен рядок якого складаються з фіксованої кількості елементів. Кома, що відділяє в числі цілу частину від дробової, займає в рядку пам’яті фіксоване положення – перед старшим розрядом або після молодшого.

Рис.1.13.

У першому випадку абсолютне значення числа менше одиниці – наприклад, 0,110101₂.Якщо рядок пам’яті призначений для десяти розрядів, то число в ньому запишеться так, як показано на рис. 1.13, де крайній лівий розряд відображає знак числа, а решта – розряди модуля. Вільні молодші розряди заповнюються нулями. Оскільки в розгляданому випадку в рядку пам’яті передбачається запис лише дробової частини числа, то і результати всіх операцій повинні бути з абсолютним значенням, меншим одиниці. Виконання цієї умови забезпечується вибором відповідних масштабних коефіцієнтів, на які помножуються вихідні дані. Якщо масштабний коефіцієнт вибраний невірно, то може з’явитись переповнення розрядів і поява цілої частини, яка буде втрачена, оскільки в розрядній сітці не передбачена її поява. Все це приведе до похибки в результаті, що є недоліком такого способу.

Рис.1.14.

У другому випадку, коли кома фіксується після молодшого розряду, маємо справу з цілими числами. Тоді, наприклад, число 10011₂ в рядку пам’яті розміщується в відповідності з рис. 1.14, де лівий розряд знаковий, а слідуючі за ним справа вільні розряди заповнюються нулями. В цьому випадку величина модуля є обмеженою довжиною рядку пам’яті.

Числа з плаваючою комою передбачають зображення числа з використанням мантиси, що помножається на основу системи числення у ступені, який задається порядком. Наприклад, число 200 записується у вигляді 0,2 × 10³, а число 0,000312 – як 0,312 × 10^-3. Відповідно записуються і двійкові числа. Мантиса і порядок зображаються у двійковому коді, а основою є двійка. Наприклад, число 0,111 × 2¹⁰ = 11.10₂ в десятковій системі зображається як 0,875 × 2² = 3,5₁₀ . В рядку пам’яті такі числа зберігаються у вигляді двох груп цифр: перша група – мантиса – визначає саме число, друга - порядок – місце коми в числі (рис. 1.15).

Рис.1.15.

У нульовому елементі рядка пам’яті зображається знак числа (для приведеного вище двійкового числа, що записане у рядок пам’яті - “0”). Далі задаються вісім розрядів самого числа (стовпці 1…8). Якщо воно задається меншою кількістю розрядів, то вільні елементи пам’яті справа від числа заповнюються нулями. У дев’ятому розряді зображається знак порядку, а в решті, за аналогією з мантисою, – число, що визначає порядок. При використанні такої форми запису величина числа порядку задається так, щоб перша значуща цифра мантиси не дорівнювала “0”. Така форма запису називається нормальною.

Мінімальне додатне число, що може бути записане при нормальній формі в рядку пам’яті, визначається мінімальною мантисою 0,1000..0₂ та максимальним від’ємним порядком 111..1₂. При кількості k розрядів порядку мінімальне десяткове число, що може бути записаним, визначається формулою:

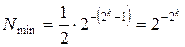. (1.15)

Максимальне число матимемо при максимальному значенні мантиси (0,111…1)₂та максимальному додатному порядку (111…1₂) = 2^k – 1, тобто

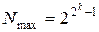. (1.16)

Діапазон D чисел, представлених в нормальній формі, як витікає з формул (1.15) та (1.16), визначається лише числом k. Наприклад, для k = 6 знаходимо:

; .

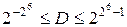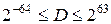Точність запису числа задається кількістю розрядівm мантиси. Якщо кількість розрядів числа перевершує відведену під мантису кількість розрядів, то число округляється до необхідної довжини. Правило округлення двійкових чисел в цьому випадку таке: якщо старший розряд у частині слова, що відкидається, є одиницею, то до молодшого розряду мантиси додається одиниця. При такому округленні абсолютна похибка e зображення мантиси не перевершує половини вагового коефіцієнта молодшого розряду мантиси, що зберігається, тобто:

.

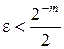Враховуючи, що при нормальній формі запису мантиса не може бути меншою 0.5, відносна похибка η:

.

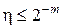Наприклад, при m = 24 маємо:

.

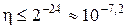У сучасних цифрових системах для зображення чисел з плаваючою комою використовується рядок довжиною чотири байти. При цьому 23 розряди задають мантису, а 7 – величину порядку. Діапазон чисел, що зображуються, складає від ± 2¹²⁷ до ± 2^-127.

Використання чисел з плаваючою комою суттєво розширює і спрощує зображення чисел, але виконання операцій над такими числами більш складне, ніж над числами з фіксованою комою.