Основное уравнение лопастных машин. Уравнение Эйлера.

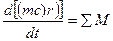(13)

Введем обозначения:

N - мощность на валу рабочего колеса;

m - секундная масса жидкости;

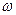- угловая скорость рабочего колеса;

М - внешний момент (на валу рабочего колеса)

М₁- момент количества движения массы жидкости на входе в рабочее колесо;

М₂ - момент количества движения массы жидкости на выходе из рабочего колеса;

N - частота вращения вала рабочего колеса;

Н_т- теоретический напор при бесконечно большом числе лопастей.

Из плана скоростей при вращении рабочего колеса по часовой стрелке следует:

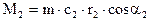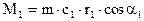, (14)

Согласно закону об изменении момента количества движения массы жидкости можно записать:

M = M₂ - M₁.

M = M₂ - M₁ = m×(r₂×c_2u - r₁×c_1u) = . (15)

Известно, что r₁×w = u₁, r₂×w = u₂, M = (16)

Умножим левую и правую части уравнения на w, а величину мощности выразим r×g×Q_T×H_T

m×(r₂×w×c_2u - r₁×w×c_1u) = r×g×Q_T×H_T

Тогда, решая уравнение относительно Н_т, получим \

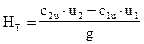, м. (17)

Анализ этого уравнения показывает, что увеличить напора насоса можно разными путями:

1. путем увеличения окружной скорости на выходе из колеса u₂. Для этого можно увеличивать количество оборотов и диаметр рабочего колеса, т.к. ;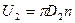

2. путем уменьшения угла a₂. При этом величина проекции абсолютной скорости движения жидкости на окружную

С_2И= U₂ 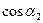будет увеличиваться. Теоретически максимальное значение С_2И= U₂ будет при угле a₂ =0, но при этом подача насоса будет равна нулю. Поэтому при конструировании центробежных насосов чаще всего принимается a₂ =8…12⁰.

3. при неизменных параметрах потока на выходе из рабочего колеса напор насоса можно увеличить путем уменьшения U₁ С_1u. Величину U₁ уменьшать не имеет смысла, потому что при этом еще больше уменьшится величина U₂. Поэтому при конструировании насосов стремятся уменьшить величину С_1u.

Для случая радиального входа жидкости в рабочее колесо, когда a₁=90 и С_1u=0, уравнение Эйлера принимает вид

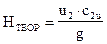(18)

Принимая во внимание, что U₂=p×D₂×n₂ формулу (1) можно записать в виде

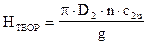(19)

Исходя из этого за счет D₂, n и C_2u можно получить сколь угодно большой напор. Однако в реальных условиях из-за ограничения перечисленных величин повышение удельной энергии на одном колесе насоса не превосходит 5000...7000 Дж/кг, что соответствует напору 500...700 м. Диаметр рабочего колеса помимо условий прочности ограничивается потерями на трение его дисков о жидкость. Частота вращения рабочего колеса лимитируется условиями прочности вала и явлением кавитации, которая может возникнуть при больших скоростях жидкости.

При конечном числе лопастей эпюра относительных скоростей в каналах рабочего колеса получится неравномерной, следовательно, будет иметь место разность давлений по обе стороны стенок лопастей. К этому следует добавить, что на характер распределения скоростей в реальном потоке оказывает влияние также форма каналов и вязкость жидкости. Суммарное влияние этих факторов учесть теоретически не представляется возможным. Чтобы применить к реальным потокам и реальным рабочим колесам результаты, полученные на основании струйной теории Л.Эйлера, вводятся опытные поправочные коэффициенты.

Теоретически напор при бесконечном числе лопаток больше напора при конечном числе лопаток и влияние числа лопастей учитывается коэффициентом Г.Ф.Проскуры

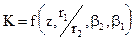, (20)

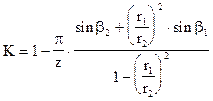, (21)

где z - количество лопаток в рабочем колесе, шт.

Обычно у центробежных насосов Z = 6...12 при этом К = 0.75...0.9.

Потери напора в насосе характеризуются гидравлическим КПД, который принимается равным 0.8...0.95.

Действительный напор насоса равен

H_д = H_T×K×h_г (22)

Пользуясь уравнением Эйлера, определим из каких частей, слагается теоретический напор насоса. Преобразуем уравнение таким образом, чтобы в него после исключения С_2u и С_1u вошли относительные, переносные и абсолютные скорости на входе и выходе из колеса. Из треугольника скоростей на основании теоремы косинусов следует:

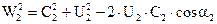(23)

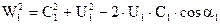(24)

Учитывая, что С₂×cosa₂ = C_2u, а С₁×cosa₁ = C_1u

Находим из уравнений

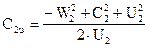
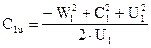
Подставим полученные уравнения в уравнение Эйлера (17)

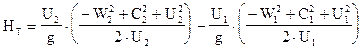
После преобразований получим

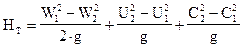(25)

Сумма первых двух членов уравнения называется статическим напором H_т.ст, а третий член уравнения называется динамическим напором H_т.дин. Для уменьшения потерь энергии в процессе преобразования динамического напора в статический последний должен составлять не менее 75...85% от полного напора. Отношение статического напора к полному напору носит название коэффициента реактивности

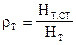(26)

Коэффициент реактивности определяется углом b₂, чем больше r_т, тем большая часть напора преобразуется в рабочем колесе в статический напор.