ЭЛЕМЕНТЫ ЛОГИЧЕСКОЙ И ИСПОЛНИТЕЛЬНОЙ ЧАСТЕЙ УСТРОЙСТВ РЗ

Элементы логической части (ЛЧ). Основными компонентами ЛЧ являются логические элементы (ЛЭ), выполняющие типовые логические операции: органов времени (ОВ), сигнальных органов, органов памяти, продлевающих действие выходного сигнала элемента, триггеров, используемых как двухпозиционные элементы, и др.

В релейно-контактных устройствах все эти элементы выполняются на электромеханических реле, в статических бесконтактных – на базе полупроводниковых приборов, первоначально в неинтегральном, а в последнее время в интегральном исполнении.

В бесконтактных схемах в качестве входных и выходных сигналов используются напряжения двух различных уровней в виде кратковременных импульсов или продолжительного сигнала, сохраняющего свое значение до тех пор, пока не изменится входной сигнал. Последний вид сигналов, называемый потенциальным, в основном и применяется в устройствах РЗ.

Логические элементы. Органы логики условно изображаются в виде прямоугольника (рис.2.72), который имеет несколько входов и один выход. На входы приходят сигналы Х от ИО или от других элементов ЛЧ. К выходу Y ЛЭ подключается нагрузка из одного или нескольких элементов ЛЧ. Кроме этого, ЛЭ имеет два входа для подачи напряжения от источника питания постоянного тока: один вход + Е_П (5-15 В) и второй – подсоединяемый к шинке нулевого потенциала логической схемы. Под воздействием входных сигналов каждый ЛЭ выполняет определенную логическую операцию:

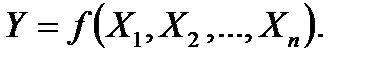(2-52)

Органы логики имеют проходную характеристику Y = f(X), аналогичную приведенной для реле на рис.1.14. Бесконтактные ЛЭ могут выполняться на полупроводниковых элементах с релейной характеристикой или на элементах, работающих в режиме переключения. Такими элементами в бесконтактных схемах являются транзисторы, работающие в двух конечных режимах: отсечки и насыщения.

Выходной сигнал ЛЭ, как у всякого реле или элемента релейного действия, носит дискретный прерывистый характер; он имеет два значения; одно – соответствующее действию и второе – недействию ЛЭ, переход из одного состояния в другое происходит практически мгновенно. Входные сигналы ЛЭ также имеют два значения и всегда дискретны. Учитывая эту особенность ЛЭ, условились обозначать уровни их значений цифровыми (логическими) символами: 0 и 1.

У бесконтактных ЛЭ логическим нулем 0 обозначаются входные и выходные напряжения низшего уровня, равные или близкие к нулю, а логической единицей 1 – сигналы высокого уровня, близкие к напряжению источника, питающего элементы ЛЧ. У контактных ЛЭ 0 соответствует разомкнутому состоянию контактов, 1 – замкнутому.

Принято логические операции, выполняемые бесконтактными ЛЭ, указывать для положительной логики, т. е. когда логический нуль на входе соответствует исходному положению органа, а срабатывание происходит при подаче единичных входных сигналов. По характеру преобразования входного сигнала в выходной ЛЭ подразделяются на неинвертирующие и инвертирующие уровни выходных сигналов. У неинвертирующего ЛЭ выходной сигнал равен логической 1 при входном сигнале, равном 1 и 0, если входной сигнал равен логическому 0. У инвертирующего ЛЭ уровень выходного сигнала всегда противоположен входному: при U_BX = 1 U_BЫX = 0 и наоборот.

В отличие от ИО к ЛЭ не предъявляется требование высокой точности уровня входных напряжений при срабатывании и возврате. От них требуется лишь четкое различение единичного сигнала от нулевого. Важным требованием является надежная отстройка от помех, исключающая их ложное действие, и надежное срабатывание при допустимых колебаниях напряжения источника питания.

Для облегчения проектирования и анализа схем была предложена теория их построения, основанная на использовании математических дисциплин, в первую очередь алгебры логики (АЛ)¹. В алгебре логики буквенными символами (А, В, С ...) обозначаются переменные величины и их функции, но, в отличие от обычной алгебры, переменные АЛ могут иметь только два различных значения, условно обозначаемые цифрами 0 и 1. Над переменными величинами АЛ производятся операции, которые записываются в виде алгебраических уравнений и формул. Основными в АЛ являются три элементарные логические операции: сложение, умножение, инверсия, называемые сокращенно, как и в формальной логике, ИЛИ, И, НЕ. Переменные величины этих выражений и их функции должны рассматриваться как значения входных и выходных сигналов ЛЭ. Первые будут обозначаться буквами X₁, Х₂, ..., Х_n, а вторые буквой Y.

Будем считать, что логические символы 0 и 1 обозначают соответственно низкий и высокий уровень U ⁰_вх и U ¹_вх и что органы логики срабатывают – выполняют свои логические операции – при изменении входных сигналов с 0 на 1 и возвращаются в исходное состояние при их изменении с 1 на 0.

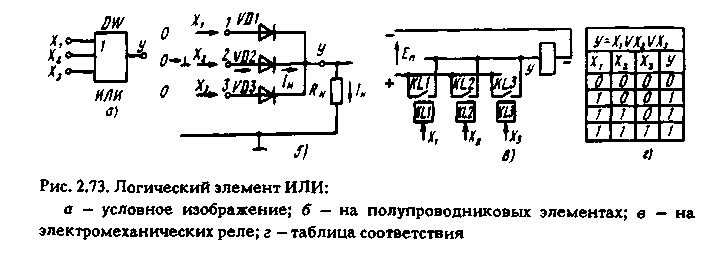
Логический элемент ИЛИ (рис.2.73) приходит в действие и его выходной сигнал Y изменяется с нулевого уровня на единичный, если хотя бы один из входных сигналов (X₁ или Х₂, или Х₃) равен логической 1.

Если же все входные сигналы Х1, Х2 и Х3 равны 0, то и выходной сигнал Y = 0 – это означает, что ЛЭ ИЛИ не действует и находится в исходном состоянии. При всех других сочетаниях значений входных сигналов Y = 1 (см. таблицу соответствия на рис.2.73, г).

Элемент ИЛИ, как показано на рис.2.73, а, изображается на чертежах прямоугольником с цифрой 1 внутри него либо обозначается буквенным символом DW.

Электронный бесконтактный ЛЭ ИЛИ может выполняться на резисторах, диодах, транзисторах. На рис.2.73, б приведена простейшая схема ИЛИ на диодах VD1-VD3.

¹ Алгебра логики разработана ирландским математиком Д. Булем и часто именуется Булевой алгеброй — она рассматривает логические функции двоичных переменных и операций с ними.

Входные сигналы X₁, X₂, Х₃ поступают на анодные входы диодов VD1, VD2, VD3. Выходом схемы является точка Y, к которой подключается нагрузка R_H при входных сигналах на уровне логического 0, недостаточного для открытия диодов, выходной сигнал Y = 0. В случае появления на одном из входов, например входе 2, единичного сигнала Х₂ = 1 в виде напряжения положительного знака +U_BX2 ≈ Е_П, диод VD2 открывается и на выходе схемы (в точке Y) появляется напряжение (с учетом нагрузки Р_H) U_BЫX = U_BX1 (пренебрегаем падением напряжения в сопротивлении R_O.Д открытого диода).

При подаче одинакового напряжения U_BX ≈ Е_П положительного знака одновременно на все три входа выходное напряжение будет таким же, как и в предыдущем случае.

На рис.2.73, в приведена контактная схема ИЛИ, которая состоит из трех промежуточных реле KL1, KL2, KL3. Контакты реле соединены параллельно, а входные сигналы X₁, X₂, Х₃ подаются на их обмотки в виде напряжения Е_П. В аналитической форме операция ИЛИ, называемая в АЛ операцией логического сложения, обозначается символическими знаками "V" либо "+" и записывается в виде уравнения

Y = X₁ V Х₂ V Х₃, либо Y = Х₁ +Х₂ + Х₃. (2.53)

Значения выходного сигнала в зависимости от всех возможных сочетаний значений X (0 и 1) даны в графах 1, 2, 3 таблицы соответствия на рис.2.73, г.

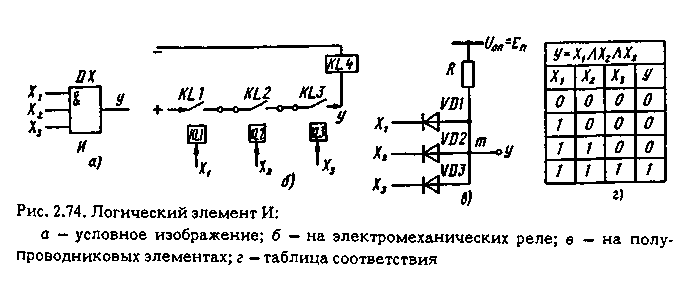
Логический элемент И (рис.2.74) приходит в действие и на его выходе возникает сигнал Y = 1 только при условии, что на всех входах ЛЭ появляется сигнал, равный 1, например: на ЛЭ с тремя входами (рис.2.74, в) Y = 1, если и Х₁, и Х₂, и Х₃ равны 1. Если же хотя бы один из входных сигналов равен логическому 0, то и выходной сигнал Y = 0. На чертежах (рис.2.74, а) ЛЭ И обозначается значком & внутри прямоугольника или буквами DX.

На рис.2.74, б приведен пример контактной схемы И с тремя входными сигналами. Схема состоит из трех промежуточных реле KL1-KL3, контакты которых соединены последовательно. Бесконтактная схема И с тремя входами Х₁ Х₂, Х₃, построенная на полупроводниковых диодах, приведена на рис.2.74, в. Если на входы схемы (т.е. на диоды VD1, VD2, VD3) поступят одновременно единичные сигналы в виде напряжения U_ВХ1, U_ВХ2, U_ВХ3 положительного знака, превышающие опорные напряжения Е_ОП, то все диоды будут заперты. В этом случае на выходе схемы (в точке Y) появится напряжение U_ВЫХ = U_ОП (логическая 1). Если хотя бы на одном входе, например на Х₁ появится сигнал низкого уровня (логический 0), при котором U_ВХ < Е_ОП, то диод VD1 откроется и на выходе схемы появится потенциал U_ВЫХ = U⁰. В аналитической форме операция И записывается по правилам логического умножения АЛ и обозначается в АЛ символическим знаком "Λ" или "•" и записывается для органа И с n входными сигналами в виде уравнения: Y = Х₁ Λ Х₂ Λ Х₃, либо Y = X₁ • Х₂ • Х₃. В таблице состояния для ЛЭ И с тремя входными сигналами значения Y = Х₁ Λ Х₂ Λ Х₃ при всех возможных сочетаниях Х₁, Х₂, Х₃ (0 и 1) приведены в таблице на рис.2.74, г.

Логический элемент НЕ преобразует входной сигнал в выходной так, чтобы он имел логическое значение, противоположное входному. Выходной сигнал (рис.2.75, а), равный логической 1, возникает, когда входной сигнал X равен логическому 0, и наоборот, Y = 0, если X = 1. Логический элемент НЕ изображается в виде прямоугольника с одним входом (рис.2.75, а), инвертирование выходного сигнала обозначается кружочком в месте его выхода или буквами DU.

Контактная схема НЕ выполняется с помощью промежуточного реле КL1 с нормально замкнутыми контактами (рис.2.76, б).

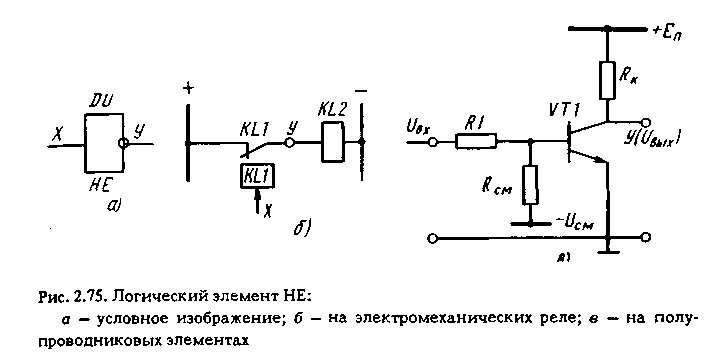
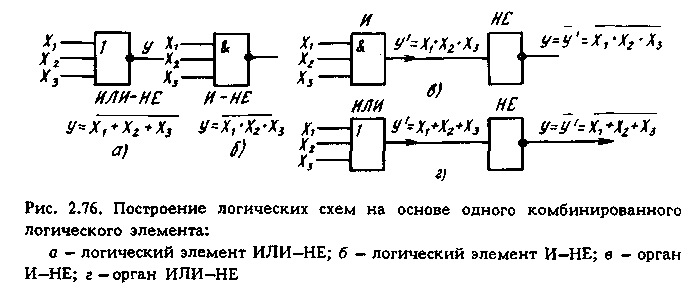
Бесконтактный орган НЕ наиболее просто выполняется посредством транзистора VT1 (рис.2.75, в), включенного по схеме с общим эмиттером и работающего в двух предельных режимах: насыщения или отсечки. Нормально эмиттер транзистора VT1 (типа n-р-n) связан с шинкой нулевого потенциала, коллектор –с +Е_П источника питания, входной сигнал U_ВХ подается на базу. Если U_ВХ соответствует логическому 0, то транзистор VT1 закрыт под воздействием напряжения смещения и находится в режиме отсечки. При этом выходное напряжение транзистора U_ВЫХ ≈ Е_П, т.е. значение выходного сигнала Y соответствует логической 1.

При подаче на вход X логической 1 в виде положительного напряжения +U_ВХ > U_б.э транзистор открывается – переходит в режим насыщения и шунтирует выход схемы, 1УВЫХ падает до нуля (сигнал Y = 1).

Операции, выполняемой логическим элементом НЕ в АЛ, соответствует операция отрицания или инверсии, она обозначается чертой над инвертируемой величиной 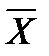и записывается в виде формулы

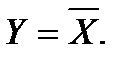(2.54)

Формула читается: Y равен не X, т.е. выходной сигнал Y равен противоположному по уровню входного сигналу. По правилам АЛ, совпадающим с правилом действия ЛЭ НЕ, Y = 1, если X = 0 и наоборот.

Комплект рассмотренных органов логики ИЛИ, И, НЕ достаточен для построения любых логических схем РЗ. Применяя в различном сочетании ЛЭ ИЛИ, И, НЕ, можно получить логическую схему любой РЗ, действующей без замедления (с t = 0), а с добавлением органов времени любой РЗ, работающей с выдержкой времени.

Построение логических схем возможно также на основе одного комбинированного ЛЭ, выполняющего операцию ИЛИ-НЕ либо И-НЕ (рис.2.76). Орган И-НЕ получается путем сочетания в единой схеме ЛЭ И с ЛЭ НЕ, как показано на рис.2.76, в. Входные сигналы Х₁, X₂, Х₃ вызывают появление сигналов на выходе элемента И: Y' = Х₁, • X₂, • Х₃. Получив этот сигнал, элемент НЕ осуществляет его инвертирование, в результате которого на выходе органа И-НЕ возникает сигнал 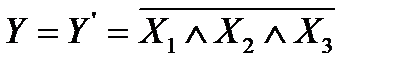. По правилам АЛ операция И-НЕ записывается в виде формулы

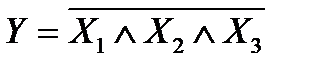, либо 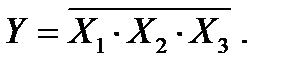(2.55)

Зависимость выходного сигнала Y от значений входных дана в графах 1, 2, 3, 7 таблицы соответствий (см. рис.2.72, б).

Орган ИЛИ-НЕ получается путем сочетания схем органов ИЛИ и НЕ (рис.2.76, г).

Операция ИЛИ-НЕ записывается в виде уравнения

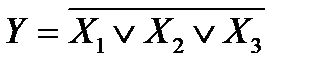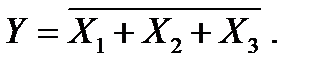либо (2.56)

Таблица состояний для органа ИЛИ-НЕ дана в графах 1, 2, 3, 6 (рис.2.72, б): оба органа И-НЕ и ИЛИ-НЕ относятся к числу инвертирующих, так как их выходные сигналы всегда противоположны по уровню вызывающим их входным сигналам.

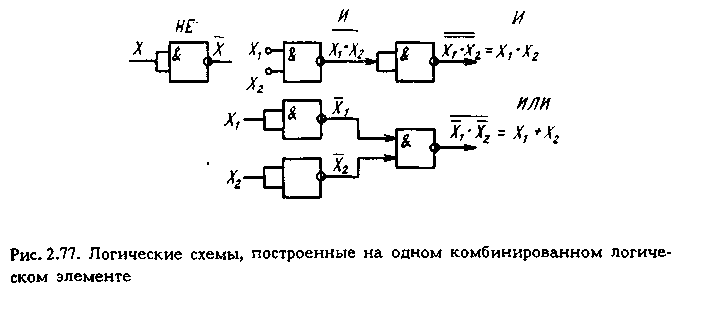
Логическая схема любой сложности может быть выполнена с помощью одного ЛЭ И-НЕ либо ИЛИ-НЕ, поскольку на основе каждого из этих органов можно осуществить элементарные логические операции ИЛИ, И, НЕ (рис.2.77).

Из рис.2.77 видно, что схемы, построенные на одном комбинированном ЛЭ, будут иметь больше элементов, однако при этом уменьшается количество типов ЛЭ (один элемент вместо трех), что удешевляет их массовое производство, поэтому комбинированные элементы на ИМС получили распространение. В основном используются схемы И-НЕ, которые имеют преимущества технологического характера по сравнению с изготовлением ИЛИ-НЕ.

Формулы и положения АЛ можно применять при рассмотрении логических схем РЗ, действующих без замедления, у которых выходные сигналы ЛЭ зависят только от сочетания одновременно возникающих входных сигналов X. Такие опера–ЛЭ и логические функции У = f(Х₁, Х₂, Х₃) принято называть комбинационными или однотактными, в отличие от многотактных, содержащих элементы времени и памяти. Для РЗ, действующих с замедлением (многотактных), АЛ может использоваться для аналитического описания всех операций, лишь с дополнениями, учитывающими в составе формул логические операции времени.