Финансово-экономические расчеты

Еще одна важная сфера приложения MS Excel связана с осуществлением финансовых расчетов. Финансовые вычисления включают в себя всю совокупность методов и расчетов, используемых при принятии управленческих решений, – от элементарных арифметических операций и до сложных алгоритмов построения многокритериальных моделей, позволяющих получить оптимальные характеристики коммерческих сделок в зависимости от различных условий их проведения. Проведение подобных вычислений – трудоемкая процедура, требующая определенной математической подготовки, а также использования большого количества справочных материалов.

С переходом к рыночным отношениям потребность в финансовых вычислениях возросла. Они стали необходимы для успешного проведения любой коммерческой сделки. В комплексе с современными методами анализа и моделирования финансовых ситуаций финансовые вычисления перерастают в новое направление организации и управления предпринимательской деятельностью – финансовый менеджмент.

Владение методами современных финансовых вычислений становится одной из основных составляющих в профессиональной подготовке предпринимателя, менеджера, банковского работника, экономиста.

На данный момент стандартный курс финансовых вычислений включает в себя следующие основные темы:

– логика финансовых операций (временная ценность денег, операции наращения и дисконтирования и т. д.);

– простые проценты (операции наращения и дисконтирования, налоги, инфляция, замена платежей);

– сложные проценты (то же и эквивалентность ставок, операции с валютой и т. п.);

– денежные потоки;

– анализ эффективности инвестиционных проектов;

– оценка финансовых активов.

Рис. 8.5.21. Вызов финансовых функций

В Excel реализовано 15 встроенных и 37 дополнительных финансовых функций. В случае необходимости применения дополнительных финансовых функций необходимо установить надстройку Пакет анализа (см. 8.5.2.2). (Список финансовых функций см. в [3].).

Напомним, что вызов Мастера функций осуществляется либо из меню Вставка > Функции – выбрать категорию Финансовые, либо с помощью одноименной кнопки на панели инструментов Стандартная. Далее в появившемся окне диалога необходимо выбрать категорию функций – и нужную функцию из категории (рис. 8.5.21).

По типу решаемых задач все финансовые функции Excel можно разделить на следующие условные группы:

– функции для анализа аннуитетов и инвестиционных проектов;

– функции для анализа ценных бумаг;

– функции для расчета амортизационных платежей;

– вспомогательные функции.

Функции каждой группы имеют практически одинаковый набор обязательных и дополнительных (необязательных) аргументов.

Дополнительную информацию по необходимой финансовой функции (расчетной формуле, реализованной в ней, списке аргументов и т. п.) пользователь может получить, вызвав контекстную справку (рис. 8.5.22).

Рис. 8.5.22. Получение дополнительной справки по функции

8.5.2.4. Финансовые функции для расчетов то кредитам,

займам и оценкам инвестиций

В финансовой практике часто встречаются операции, характеризующиеся возникновением потоков платежей, распределенных во времени. Потоки платежей, при которых выплаты (поступления) денежных средств осуществляются равными суммами через одинаковые интервалы времени, называются обыкновенным аннуитетом. Такие потоки возникают при проведении кредитно-депозитных операций, формировании различных фондов, долгосрочной аренде и т. п.

Количественный анализ таких операций сводится к исчислению следующих основных характеристик:

– текущей величины потока платежей (Present value – Pv);

– будущей величины потока платежей (Future value – Fv);

– величины отдельного платежа (payment – R);

– нормы доходности в виде процентной ставки (interest rate – r);

– числа периодов проведения операции (число лет, месяцев).

К этой группе также относятся и функции, которые позволяют эффективно осуществить расчет наиболее широко применяемых критериев эффективности инвестиционных проектов, – NPV, IRR и т. п.

Функции этой группы используют сложные итерационные алгоритмы для исчисления соответствующих показателей. При этом делаются некоторые допущения:

– потоки платежей на конец (начало) периода известны;

– для всего срока проведения операции определена оценка в виде процентной ставки, в соответствии с которой средства могут быть инвестированы.

Рассмотрим несколько примеров использования функций для решения конкретных задач.

Определение будущей стоимости

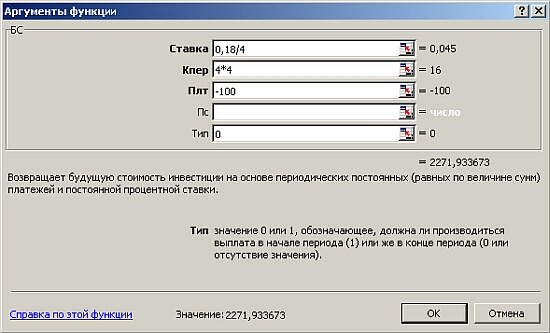
Рис. 8.5.23. Диалоговое окно ввода аргументов функции (БЗ)

Пример 1. Фирма создает фонд для погашения долгосрочных обязательств, для чего перечисляет ежегодно в течение 4 лет платежи размером 100 тыс. р. в конце каждого года, на которые начисляются сложные проценты по ставке 18% годовых, начисляемых ежеквартально. Определить величину фонда к концу срока выплат.

Для решения данной задачи необходимо выполнить следующие действия:

1. Вызвать Мастер функций.

2. Из общего списка выбрать функцию БЗ.

3. Заполнить диалоговое окно, то есть ввести необходимые аргументы функции (в поля ввода можно вводить как ссылки на ячейки, содержащие значения аргументов, так и сами значения), рис 8.5.23.

4. Завершить ввод аргументов и запуск расчета значений функции нажатием кнопки ОК.

5. При отказе работы с функцией нажать кнопку Отмена.

Дадим краткие комментарии по значениям аргументов функции БЗ:

– величина периодических выплат (поле Выплата), согласно правилам заполнения, должна быть введена со знаком минус;

– по условию задачи мы соответствующим образом скорректировали поля Норма и Число периодов, так как предусматривается ежеквартальное начисление процентов;

– значение 0 у параметра Тип принимается по умолчанию и означает, что применяется аннуитет постнумерандо (взносы в конце года), значение –1 означает аннуитета пренумерандо (взносы в начале года).

Параллельно процессу заполнения полей аргументов происходит формирование результата расчетов, окончательно он равен 2271,93. Для завершения ввода функции БЗ в ячейку рабочего листа Excel следует нажать кнопку ОК.

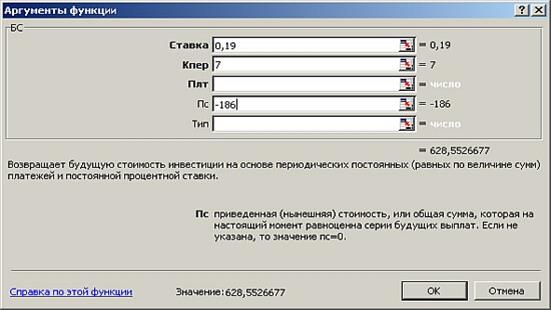
Рис. 8.5.24. Диалоговое окно функции БЗ

В результате ячейка будет содержать формулу

Необходимо отметить, что основные финансовые функции, такие как БЗ, ПЗ, НОРМА, КПЕР, используются не только для вычислений, имеющих дело с аннуитетом, но и для задач с разовыми вкладами на основе постоянной процентной ставки.

Пример 2. Банк выдает долгосрочный кредит в размере 186 тыс. р. по сложной ставке 19% годовых. Определить сумму долга через 7 лет.

Порядок действий при решении задачи тот же. Необходимо правильно заполнить поля ввода функции БЗ. Для решения этой задачи нужно заполнить не поле Выплата, а поле НЗ, так как в этом случае финансовая функция будет рассчитывать значение FV просто по формуле нахождения будущей стоимости для сложных процентов:

FV=PV(1+i)^n.

Заполним финансовую функцию БЗ следующим образом:

=Б3(0,19; 7;; -186).

На рис. 8.5.23 и 8.5.24 приведены примеры использования финансовых функций из Excel XP. В случае Excel 2000 значения вводятся в поля (норма; число_периодов; выплата; нз; тип).

Определение текущей стоимости

Для решения задач расчета текущей стоимости используются следующие функции:

– П3 (норма; число периодов; ; бс) – расчет текущей стоимости для единой суммы вклада;

– П3 (норма; число периодов; выплата; ; тип) – расчет текущей стоимости фиксированных периодических выплат;

– НПЗ (норма; значения) – расчет текущей стоимости периодических поступлений переменной величины;

– ЧИСТНЗ (ставка; значения; даты) – расчет текущей стоимости нерегулярных поступлений переменной величины. Даты должны соответствовать суммам выплат (поступлений). Расчет производится на дату, осуществления первой операции, то есть первая сумма не дисконтируется. Если нужно произвести дисконтирование, на другую дату, то необходимо первой дате в списке сопоставить выплату, равную 0.

Рассмотрим несколько простых примеров.

1. Какую сумму необходимо положить в банк, выплачивающий 13,7% годовых, чтобы через 3 года получить 250 тыс. р.?

Для решения следует использовать функцию =П3([норма:] 0,137; [число периодов:] 3; ; [бс:] -250). Ответ: 170,08. То что в квадратных скобках не вводится.

2. Платежи в фонд будут вноситься ежегодно по 200 тыс. р. в течение 4 лет с начислением на них сложных процентов по ставке 8% годовых. Определить современную сумму всех платежей с начисленными процентами.

Для решения следует использовать функцию

=П3([норма:] 0,08; [число периодов:] 4; [выплата:] -200; [тип:] 0).

Ответ: 662,43.

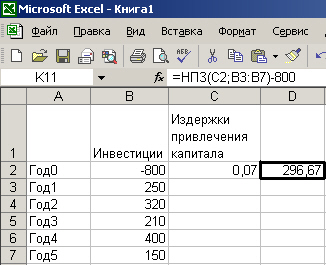
Рис. 8.5.25. Нахождение NPV

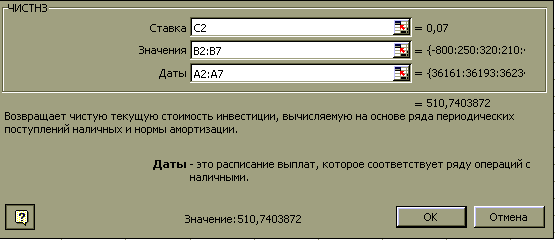
Рис. 8.5.26. Нахождение NPV на дату выплаты

3. Инвестиции в проект составляют 800 тыс. р. В последующие 5 лет ожидаются следующие годовые доходы по проекту: 250; 320; 210; 400; 150 тыс. р. Издержки привлечения капитала 7%. Рассчитать чистую текущую стоимость проекта.

Для решения следует использовать функцию

=НПЗ([норма:] 0,07; [значения: –] диапазон_ячеек_со_значениями_доходов_ по_ проекту).

Для нахождения непосредственного значения NPV необходимо вычесть начальную инвестицию.

Ответ: 296,67 (рис. 8.5.25).

Положительное значение NPV является показателем того, что проект приносит чистую прибыль своим инвесторам после покрытия всех связанных с ним расходов.

4. Та же задача, но заданы конкретные даты: выплата – 1.01.99 г., поступления – 2.02.99 г., 15.03.99 г., 25.03.99 г., 10.04.99 г., 20.04.99 г. соответственно.

Для решения следует использовать функцию ЧИСТНЗ. Порядок задания ее аргументов показан на рис. 8.5.26. Заметим, что значение начальной выплаты должно быть введено со знаком минус.

Ответ: 510,74, результаты расчета представлены на рис. 8.5.27.

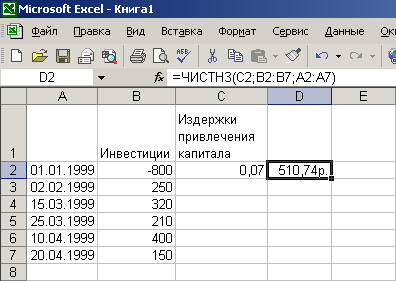
Рис. 8.5.27. Нахождение NPV на дату первой выплаты