Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как угол поворота радиуса - вектора за единицу времени
Вращательные движения
Вращательное движение материальной точки - движение материальной точки по окружности. Во время равномерного вращательного движения тело совершает движение по окружности с одинаковой скоростью, но с изменяющимся направлением. Например, такое движение совершают стрелки часов по циферблату.
• 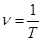
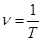
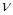
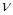
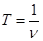
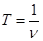
Время, за которое тело полностью делает один полный оборот по окружности, называется периодом вращения - T. - частота вращения - число оборотов тела в единицу времени. Мера вращательного движения: угол φ, на который повернётся радиус-вектор точки в плоскости, нормальной к оси вращения.
Равномерное вращательное движение: за любые равные промежутки времени тело поворачивается на одинаковые углы.
Радиан.
• При вращательном движении основной единицей измерения углового перемещения является радиан. 2π радиан = 360° - полная окружность
• π радиан = 180° - половина окружности
• π/2 радиан = 90° - четверть окружности
• Чтобы перевести градусы в радианы, необходимо значение угла разделить на 360° и умножить на 2π.
• Например: 45° = (45°/360°)·2π = π/4 радиан
• 30° = (30°/360°)·2π = π/6 радиан
• 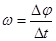
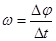
Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как угол поворота радиуса - вектора за единицу времени
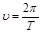
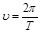
Во время равномерного вращательного движения меняется только направление вектора линейн скорости, но не величина! Поэтому линейное ускорение = 0. Изменение линейной скорости поддерживается центростремительным ускорением, которое направлено к центру окружности вращения перпендикулярно вектору скорости - aцс. Чтобы вычислить линейную скорость тела, необходимо разделить перемещение на время, т.е. длину окружности на период вращения:
• 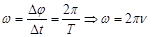
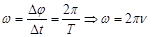
При равномерном вращении за период T радиус-вектор точки повернётся на угол 2π. Тогда угловая скорость точки равна
• Угловая скорость точки не зависит от радиуса окружности!
• 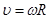
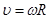
Дата добавления: 2016-09-26; просмотров: 1564;











