Примеры численного моделирования цепей первого порядка

Из курса математики известно, что интеграл - это есть площадь, заключённая между графиком функции и осью абсис, т.е. для того чтобы найти значение определённого интеграл функции 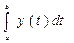, необходимо найти площадь S (рис. 4.8). Эту площадь можно найти аналитически, решив интеграл, или численно. Существует различные численные методы интегрирования, но мы рассмотрим только два простейших: метод прямоугольников и метод трапеций. Суть методов поясним с помощью рис. 4.8. Значение интегралла можно приближённо рассчитать, найдя сумму площадей прямоугольнков (рис. 4.8,b) или сумму плащадей трапеций (рис. 4.8,c).

,

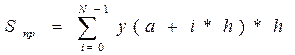
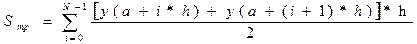где h = (b-a)/N; N –произвольное целое число. Понятно, что чем больше N, тем меньше шаг h и тем точнее результат численного интегрирования.

Рис. 4.8. Пояснения к методам численного интегрированния: а) точное значение интеграла b) вычисление значениея интеграла методом прямоугольников; с) вычисление значениея интеграла методом трапеций

Методы численного интегрирования широко применяются при моделировании цепей и сигналов. Приведём два простейших примера. Найдём выражения для численного расчёта токов и напряжения на реактивных элементах в цепях, изображённых на рис. 4.9. Будем считать, что в момент времени t = 0 значение независимого источника напряжения e(t₀) изменилось с 0 до 1 В (единичный скачёк), R =10кОм, C = 10 мкФ, L = 10мкГ.

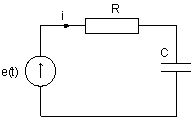
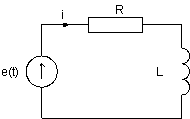
Рис. 4.9. Моделируемая RС и RL цепь

Как известно, токи и напряжения на ёмкости C и индуктивности L связанны соотношениями:

.

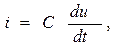
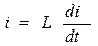Проинтегрировав оба уравнения, получим

.

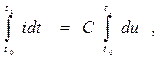
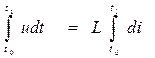Применяя метод трапеции к левым частям равенств и находя интеграл в правых частях, получим итерационные выражения:

,

,

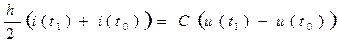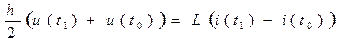где h – шаг численного интегрирования. Выражая напряжение через ток, получим для ёмкости С и индуктивности L итерационные выражения:

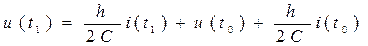, (4.1)

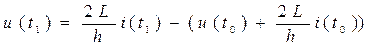. (4.2)

Запишем уравнения, описывающие зависимость токов и напряжений в RC и RL цепях (первый закон Киргоффа, закон коммутации, компонентные уравнения элементов цепи)

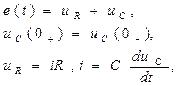
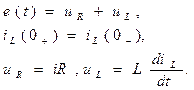
Подставив в первый закон Киргоффа вместо u_C и u_L полученные выше итерационные выражения, запишем:

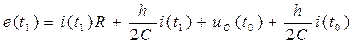, (4.3)

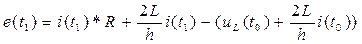. (4.4)

Выберем значение шага интегрирования h = 0.1RC = 0.1мc как одну десятую от постоянной времени цепи. Исходя из законов коммутации, определим значение токов и напряжений на реактивных элементах в момент коммутации (t = t₀ = 0).

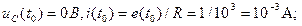(4.5)

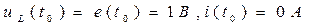. (4.6)

Подставим численные значения в выражения и найдём значение тока i(t₁) в RC и RL цепи.

,

.

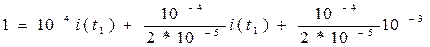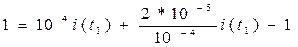Далее находим из выражения (4.1, 4.2) значение u_C(t₁) и u_L(t₁), подставляем их в выражение (4.3, 4.4 ) вместо u_C(t₀) и u_L(t₀), а вместо i(t₀), естественно, i(t₁), и находим i(t₂) и т.д.

Программа, реализующая расчёт напряжения и тока на ёмкости С RC-цепи, приведённой на рис. 4.9, представлена ниже. Она расчитывает первые сорок значений напряжения и тока на ёмкости C. Графики напряжения и тока на С при R =10кОм, C = 10 мкФ, Е = 1В приведены на рис 4.10.

//Программа 4.6

#include "stdafx.h"

#include <iostream>

void main(){

double R, C, E, t = 0;

std::cout<<"\nInput R = ";std::cin>>R;

std::cout<<"\n Input C = ";std::cin>>C;

std::cout<<"\n Input a size jump E = ";std::cin>>E;

double Uc0 = 0, Ic0 = E/R, h = 0.1*R*C;

double Uc1, Ic1;

std::cout<<"\n t = "<<t<<" E = "<<E<<" Uc1 = "<<Uc0<<" Ic1 = "<<Ic0;

for(int i = 0; i < 40; i++){

Ic1 = (E - Uc0 - h/(2*C)*Ic0)/(R + h/(2*C));

Uc1 = h/(2*C)*Ic1 + Uc0 + h/(2*C)*Ic0;

t = t+h;

std::cout<<"\nt="<<t<<"E="<<E<<"Uc1="<<Uc1<<"Ic1="<<Ic1;

Uc0 = Uc1; Ic0 = Ic1;

}

getchar();

}

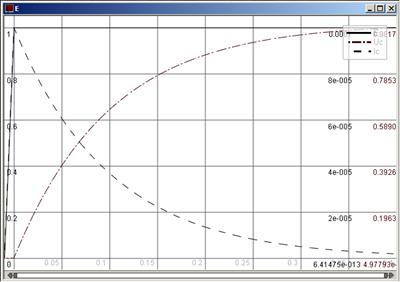
Рис. 4.10. Графики напряжение и ток на C при R =10кОм, C = 10 мкФ, Е = 1В

Написать программу и рассчитать значение тока и напряжения на индуктивности L в RL цепочки по полученным выражениям (4.4) и (4.6) рекомендую студентам самостоятельно.