Спин электрона. Спиновое квантовое число.
О. Штерн и В. Герлах, проводя прямые измерения магнитных моментов, обнаружили в 1922 году, что узкий пучок атомов водорода, заведомо находящихся в s-состоянии, в неоднородном магнитном поле расщепляются на два пучка. В этом состоянии момент импульса электрона равен нулю. Магнитный момент атома, связанный с орбитальным движением электрона, пропорционален механическому моменту, поэтому он равен нулю, и магнитное поле не должно оказывать влияния на движение атомов водорода в основном состоянии, т. е. расщепления быть не должно. Однако в дальнейшем при применении спектральных приборов с большой разрешающей способностью было доказано, что спектральные линии атома водорода обнаруживают тонкую структуру (являются дублетами) даже в отсутствие магнитного поля.
Для объяснения тонкой структуры спектральных линий, а также ряда других трудностей в атомной физике американские физики Д. Уленбек и С. Гаудсмит предположили, что электрон обладает собственным неуничтожимым механическим моментом импульса, не связанным с движением электрона в пространстве, - спином.
Спин электрона (и всех других микрочастиц) – квантовая величина, у нее нет классического аналога, это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.
Если электрону приписывается собственный механический момент импульса (спин) Ls, то ему соответствует собственный магнитный момент pms. Согласно общим выводам квантовой механики, спин квантуется по закону
Ls = 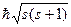 ,
,
где s – спиновое квантовое число.
По аналогии с орбитальным моментом импульса, проекция Lsz спина квантуется так, что вектор Ls может принимать 2s + 1 ориентаций. Так как в опятах Штерна и Герлаха наблюдались только две ориентации, то 2s + 1 = 2, откуда s = ½. Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением, аналогичным (3.8):
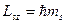 ,
,
uде ms – магнитное спиновое квантовое число; оно может иметь только два значения ms = ±1/2.
Таким образом, опытные данные привели к необходимости характеризовать электроны (и микрочастицы вообще) добавочной внутренней степенью свободы. Поэтому для полного описания состояния электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать еще магнитное спиновое квантовое число.
Дата добавления: 2020-12-11; просмотров: 617;











