Приближенные решения задач устойчивости пластин

Рассмотрим приближенные решения, основанные на использовании энергетического подхода к задачам устойчивости пластин.

Как и в задачах устойчивости стержней, здесь могут быть использованы критерии устойчивости в форме Брайана или в форме Тимошенко.

Начнем с критерия в форме Брайана, для применения которого необходимо знать докритическое напряженное состояние пластины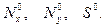

Запишем выражение приращения полной потенциальной энергии пластины при ее выпучивании.

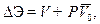(15.1)

где 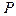- параметр нагрузки,

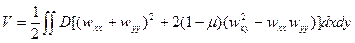(15.2)

- энергия изгиба пластины, представляющая собой работу изгибных напряжений, а

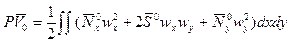(15.3)

- работа постоянных по толщине пластины докритических напряжений на деформациях срединной плоскости

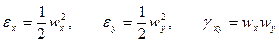(15.4)

за счет изгиба пластины.

Напомним, что возможны два способа поиска точек бифуркации.

I. Из условия стационарности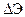

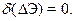(15.5)

2. Из условия

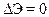(15.6)

при дополнительном требовании минимума нагрузки.

Из условия (15.5) вытекают точные уравнения устойчивости пластины и естественные граничные условия на ее кромках.

Уравнения Эйлера для функционала (15.1)-(15.3)

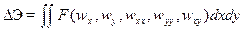(15.7)

записывается так

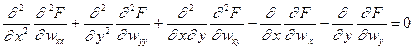(15.8)

или в развернутом виде

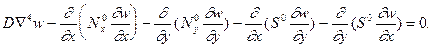(15.9)

Это основное линеаризованное уравнение устойчивости пластин (13.13).

Естественные граничные условия для функционала (15.7) записываются так

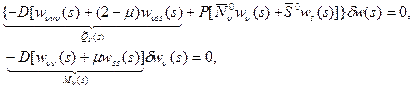(15.10)

где 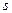- дуга контура, а индексами 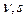обозначены производные по нормали и касательной к контуру.

Легко видеть, что первое условие тождественно выполняется на тех участках контура, где заданы прогибы 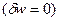, а при произвольных прогибах из него следует статическое граничное условие (13.21). Второе условие выполняется при заданном угле поворота 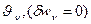, а при раскрепощенном угле поворота из него вытекает статическое условие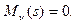

Перейдем к энергетическому критерию в форме Тимошенко. Опуская обоснование этого критерия, с которым можно ознакомиться в [I] , приведем его вид для случая, когда пластина нагружена только контурными усилиями 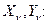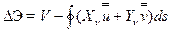. (15.11)

Здесь 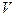по-прежнему определяется выражением (15.2), а 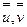- перемещения второго порядка малости, которые необходимо предварительно найти, выразив их через функцию прогиба 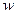из уравнений

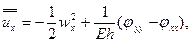
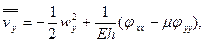(15.12)

где 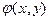- функция, в свою очередь удовлетворяющая уравнению

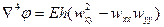(15.13)

и однородным граничным условиям на контуре

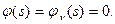(15.14)

Критерии Брайана и Тимошенко эквивалентны.

Критерий Брайана удобнее, когда предварительное напряженное состояние достаточно простое.

Критерий Тимошенко предпочтителен для построения приближенных решений сложных задач. Если, например, функция 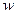ищется в виде некоторого ряда

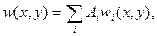
то уравнение (15.13) с условиями (15.14) полностью идентично задаче изгиба защемленной по контуру пластины при заданной (с точностью до 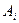) нагрузке. Такие решения хорошо разработаны. Зная их, то есть зная 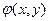, легко из (15.12) найти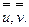

Однако, для решения задач термоупругой устойчивости, где контурная нагрузка 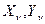отсутствует, критерий Тимошенко в форме (15.11) не применим.

Полученные выражения служат также для построения приближенных решений.

Метод Релея-Ритца

Возможные прогибы пластины задаются в виде

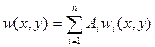, (15.15)

где 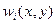- функции, обязанные удовлетворять однородным кинематическим граничным условиям и прочим сформулированным требованиям.

После подстановки (15.15) в (15.1)-(15.3) и интегрирования, получаем квадратичную зависимость

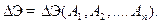(15.16)

Условия стационарности функции (15.16)

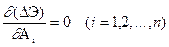(15.17)

дают систему 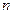линейных, однородных алгебраических уравнений. Нетривиальное решение возможно лишь в случае равенства нулю определителя этой системы.

При однопараметрическом задании нагрузки это будет характеристическое уравнение степени 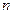относительно параметра. Наименьший из этих корней дает приближенное значение .

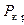Возможна и другая эквивалентная редакция поиска 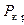- на основе условия (15.6). Из этого условия с учетом (15.1) следует

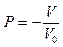(15.18)

Минимум величины 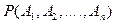ищется каким-либо численным методом.

Следует еще раз подчеркнуть, что для того, чтобы воспользоваться энергетическим критерием в форме (15.1)-(15.3) необходимо предварительно решить плоскую задачу о докритическом напряженном состоянии.