Решение в одинарных тригонометрических рядах

Для пластин, шарнирно опертых по двум противоположным сторонам с произвольными условиями по двум другим сторонам может быть построено точное решение, аналогичное решению Леви в теории изгиба пластин.

Прогиб 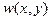представляется в виде

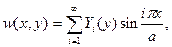(14.9)

где 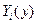- искомые функции.

После подстановки в (14.1) получаем

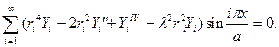
Логика дальнейших рассуждений такая же, как и при решении в одинарных рядах.

Нетривиальные решения возможны лишь при равенстве нулю хотя бы одной из скобок

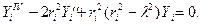(14.10)

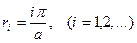
Мы получили полностью распавшуюся систему обыкновенных дифференциальных уравнений.

Общее решение каждого из них записывается в виде

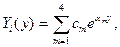(14.11)

где 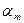- корни характеристического уравнения

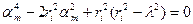
принимают значения

.

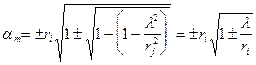Оценим эти корни. Для случая цилиндрического изгиба справедлива формула (14.2), которая при шарнирном опирании кромок 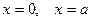дает

.

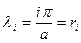Логично предположить, что бесконечная пластина будет иметь меньшие критические напряжения, чем конечная при любом закреплении кромок 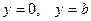. Тогда 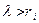и общее решение (14.11) уместно переписать в виде

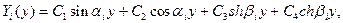(14.12)

где

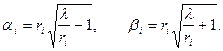
Строго говоря, высказанного предположения можно было и не делать. Если 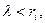то 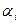окажутся чисто мнимыми, и тригонометрические функции изменятся на гиперболические от действительного аргумента.

Общее решение (14.12) надо подчинить однородным граничным условиям на кромках 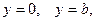предварительно преобразовав эти условия, наложенные на 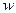, в условия на .

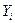В результате получим систему четырех однородных алгебраических уравнений относительно констант 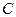. Приравняв нулю определитель этой системы, получим уравнение для отыскания собственных значений .

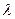Пусть кромки пластины 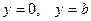жестко защемлены. Тогда задача симметрична, и логично перейти к центральной координате или, что то же самое, произвести в (14.12) замену 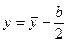с тем, чтобы из соображений симметрии обнулить две константы из четырех. Однако, отбросить при этом функции, кососимметричные относительно 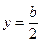, было бы неверным, поскольку симметрично закрепленная пластина может потерять устойчивость как по симметричной, так и по кососимметричной форме. Ясно, что реализуется одно состояние из двух: либо

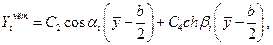
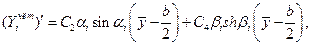(14.13)

либо

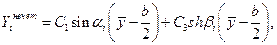
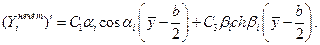(14.14)

В обоих вариантах надо выполнить только два граничных условия. Например, при жестком защемлении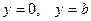

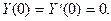(14.15)

Подчиняя (14.13) условиям (14.15), получаем

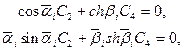(14.16)

где

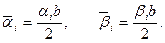
Приравняв к нулю определитель системы (14.16), получаем трансцендентное характеристическое уравнение

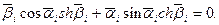(14.17)

Аналогично для функций (14.14):

,

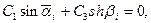
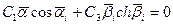откуда

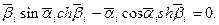(14.18)

Корни уравнений (14.17), (14.18) приходится искать численно, организуя перебор 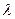. Критические напряжения будут соответствовать наименьшему из корней этих двух уравнений.