Устойчивость пластин при сдвиге

Еще один простой и в то же время достаточно распространенный вариант напряженного состояния пластины - чистый сдвиг: .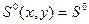

Строго говоря, такое состояние порождается равномерно распределенными по контуру касательными усилиями. Однако этот случай является широко распространенной расчетной моделью для стенок лонжеронов при условии, что нормальными напряжениями в них можно пренебречь, а также для панелей кессонов при кручении.

Линеаризованное уравнение устойчивости (13.17) для этого случая

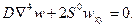(16.1)

Энергетический критерий устойчивости в форме Брайана (15.1)

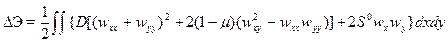. (16.2)

Как и при сжатии, начнем исследование с достаточно длинной пластины 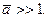Легко видеть, что решение типа цилиндрического изгиба

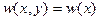
здесь не проходит, поскольку в (16.1) при дифференцировании по координате y исчезает член, содержащий .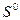

Решение вида

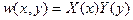
также не проходит, т.к. после подстановки (16.2) в (16.1) переменные не разделяются.

Решение в одинарных рядах

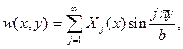
удовлетворяющее условиям шарнирного опирания длинных кромок пластины, после подстановки в (16.1) дает

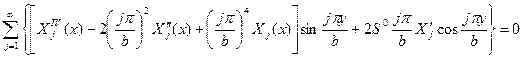(16.3)

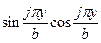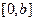Поскольку функции на не ортогональны, уравнение может привести только к бесконечной связанной системе дифференциальных уравнений относительно разных 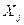, что мало привлекательно для решения.

Форму, в которой можно искать приближенное решение для длинной пластинки, подсказывает эксперимент (рис.16.1) - пластина теряет устойчивость с образованием косых волн. Такую форму можно аппроксимировать функцией

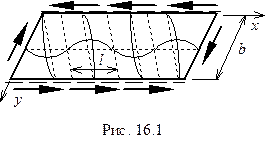
(16.4)

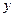обнуляющейся на линиях , образующих с осью угол 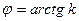и отстоящих друг от друга на 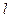. Функцию 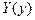следует задать так, чтобы она отвечала кинематическим граничным условиям на продольных кромках.

Например, при их шарнирном закреплении

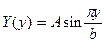. (16.5)

Это традиционное представление не удовлетворяет условию

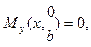(16.6)

поскольку

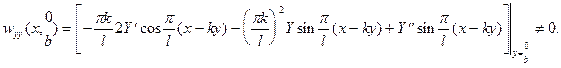Условие (16.6) можно выполнить, задав, например, 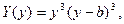но тогда, кроме , будет и 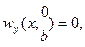то соответствует защемлению без краевого момента, а это противоречит физическому смыслу задачи.

Поскольку условие (16.6) статическое и, следовательно, его выполнять не обязательно, остановимся на представлении (16.5).

Теперь можно воспользоваться методом Релея-Ритца или методом Бубнова-Галеркина, сохранив контурный интеграл в (15.20).

Воспользуемся первым. Подставим (16.4), (16.5) в (16.2).

Приравняв 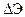нулю, найдем

(16.7)

Параметры 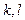найдем из условия минимума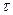

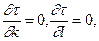
что дает

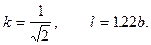(16.8)

Таким образом,

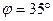(16.9)

Подставляя (16.8) в (16.7), находим

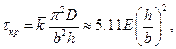(16.10)

где

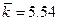. (16.11)

Для пластинки, защемленной по продольным кромкам, задав

,

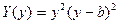получим .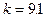

Теперь рассмотрим пластину с сопоставимыми размерами сторон. Пусть она закреплена по всему контуру шарнирно.

Тогда представление Навье

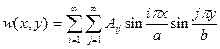(16.12)

удовлетворяет всем граничным условиям. Остается только найти 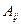, подчинив (16.12) уравнению (16.1)

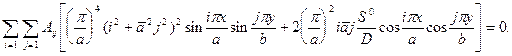(16.13)

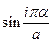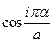Поскольку, как отмечалось, функции и на 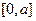не ортогональны, то из (13) после умножения на 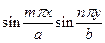следует

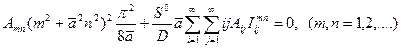(16.14)

где

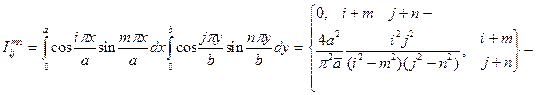нечетны.

Мы получили бесконечную связанную систему алгебраических уравнений. Приближенные собственные значения параметра можно найти лишь, “усекая” систему до конечного числа 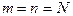. Тогда, приравняв нулю определитель системы, мы получим характеристическое уравнение степени 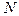относительно 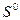. Аналитически это можно сделать лишь при очень малых 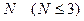, что еще не дает надежного результата. Поэтому процесс ведут численно. Задаются 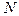и перебором 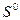ищут наименьшее, при котором 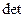будет близок к нулю с заданной степенью точности. Затем, последовательно увеличивают 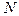и каждый раз находят 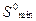. Поиск прекращают, когда значения 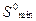становятся стабильными.

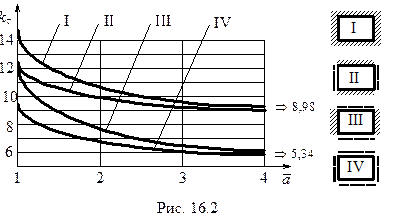
В общем случае критические напряжения могут быть записаны формулой

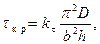(16.15)

где - графические.

При увеличении 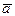условия закрепления коротких сторон перестают сказываться, и значения 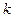становятся стабильными, причем довольно близкими к полученным ранее для бесконечно длинной пластины.

Кривые на рис.16.2 можно аппроксимировать зависимостями

(16.16)

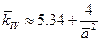. (16.17)

При иных граничных условиях подбор достаточно большого числа 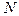аппроксимирующих функций затруднен.

Если мы хотим получить оценку критических напряжений “в запас прочности”, то аппроксимация должна отвечать менее жестким условиям закрепления, чем в расчетной модели.