Кодирование факторов

Выбор факторного пространства

Напомним, что под выбором фак­тор­но­го пространства понимается этап пла­нирования эксперимента, на котором выбираются значения факторов в центре эксперимента (средние значения, нуле­вые уровни) и их диапазоны варь­иро­ва­ния.

Для исследуемого механизма (и вообще для рычажных механизмов АКУ) это довольно сложная задача, требующая большого терпения. Дело в том, что механизм вследствие больших зна­чений передаточных отношений зве­ньев очень чувствителен к малейшему (на единицы мм) изменению значений координат шарниров (и зависящих от них длин звеньев). В рассматриваемом слу­чае многократным предварительным мо­делированием и отсечением тех об­лас­тей, где наблюдается либо “вре­за­ние” шарниров в корпус АКУ, либо раз­ры­вы звеньев, либо их сжатие и т.д. по­добраны следующие значения ос­нов­но­го уровня факто­ров:

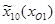=425 мм; 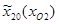=600 мм;

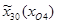=1425 мм; 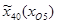=1595 мм;

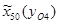=-75 мм; 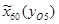=-145 мм;

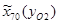=-145 мм; 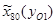=-75 мм;

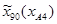=50 мм; 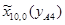=-105 мм;

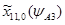=0,35; 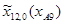=1050 мм;

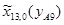=-105 мм; 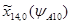=0,35;

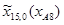=1635 мм; 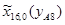=-85 мм;

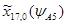=0,65.

Подобраны также диапазоны их варьирования:

J₁= J₂= J₃= J₄= J₅= J₆= J₇= J₈= J₉= J₁₀= J₁₂= J₁₃= J₁₅= J₁₆=5 мм;

J₁₁= J₁₄= J₁₇=0,1.

Кодирование факторов

Напомним, что кодирование факторов применяется для «обезличивания» эксперимента. Эксперимент планируется для кодированных значений, а ставится для их натуральных значений.

Для факторов с непрерывной область определения (в данном случае это именно так) кодирование осуществляется с помощью соотношений:

,

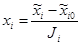где х_i – кодированное значение,

х_i0 – натуральное значение фактора.

Выбор плана эксперимента

В результате реализации плана эксперимента модель параметра оптимизации j должна быть получена в виде:

.

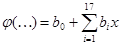Для 17-ти факторов требуется поставить эксперимент из 2¹⁷ (131272) опытов. Очевидно, что это нереально.

Учитывая, что полный факторный эксперимент обладает существенной избыточностью опытов, для определения коэффициентов линейной модели можно обойтись гораздо меньшим числом опытов. Для этого воспользуемся дробной репликой. Так как определяемых коэффициентов всего восемнадцать, то можно воспользоваться репликой, в основе которой ПФЭ 2⁵ (т.е. 32 опыта). Таким образом, в данном случае используется 2^17-12 реплика.

В плане 25 всего 31 столбец (х₁, х₂, …, х₅, х₁х₂, …, х₁х₅, х₂х₃, …, х₂х₅, …, х₁х₂х₃х₄х₅). Плюс столбец для фиктивного фактора х₀. Итого 32.

Столбцы, в которых содержатся значения парных, тройных и т.д. взаимодействий (их 26), могут быть использованы для формирования значений факторов х₆…х₁₇).

При формировании дробной реплики важным моментом является обеспечение как можно более высокой разрешающей способности плана. Поэтому желательно использовать столбцы, начиная справа, т.е. х₁₇ ставим в соответствие значения крайнего правого столбца и далее влево(при этом для рассматриваемого случая исключаются парные взаимодействия).

Таким образом, имеем следующие генерирующие соотношения реплики:

х₆=х₁х₂х₃; х₇=х₁х₂х₄; х₈=х₁х₂х₅;

х₉=х₁х₃х₄; х₁₀=х₂х₃х₄; х₁₁=х₂х₄х₅;

х₁₂=х₁х₂х₃х₄; х₁₃=х₁х₂х₃х₅;

х₁₄=х₁х₂х₄х₅; х₁₅=х₁х₃х₄х₅;

х₁₆=х₂х₃х₄х₅; х₁₇=х₁х₂х₃х₄х₅;

Умножив первое соотношение на х₆, второе на х₇ и т.д. последнее на х₁₇ получим выражения для обобщающих контрастов, перемножив которые получим выражение для обобщающего определяющего контраста плана, который позволяет определить систему смешивания коэффициентов линейной модели.

Оказывается, что при принятом подходе к проектированию реплики, ООК равен произведению всех! факторов, т.е.

1=х₁х₂…х₁₃х₁₄х₁₅х₁₆х₁₇.

Разрешающая способность такой реплики равна XVII. Это значит, что линейные коэффициенты модели смешиваются с взаимодействиями только 16-го порядка! Очевидно, что таким взаимодействием можно пренебречь (весьма сложно представить ситуацию, при которой для сложной системы взаимодействие 16 факторов будет более значимым, чем каждый фактор в отдельности).

Реализация плана эксперимента