МЕТОД РАСЧЕТА ТЕЧЕНИЯ В КАНАЛЕ

Течение внутри канала предполагается сверхзвуковым вдоль оси канала. Следовательно, в этом направлении система уравнений Эйлера является гиперболической относительно пространственной координаты, а решение может быть получено посредством пошагового интегрирования по координате z.

Геометрия канала описывается зависимостью: r = R(z),т.е. предполагается, что канал осесимметричный. Преобразование координат должно модифицировать. Перейдем к новым независимым переменным по формулам:

x = x, 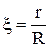, j = j(4.1)

Преобразование (4.1) обеспечивает нормировку расчетной области в радиальном направлении. Система уравнений Эйлера (глава 3) в новых переменных имеет вид:

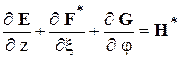(4.2)

где F^* = f₁E+f₂F, H^* = H-gE, 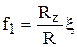, , 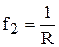, 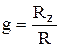нижний индекс «z» - производная функции по z.

Опишем построение расчетной сетки в случае расчета течения в канале с крестообразным оперением. Для выделения оперения строится четыре области - рис.4.1. На рисунке изображены сетки во всех областях, кроме одной, для которой сетка приведена только в одном – конечном сечении. Количество секторов по углу (в рассматриваемом случае - четыре) определяется количеством плоскостей, в которых расположено оперение. Например, если рассматривается трехконсольное оперение, то выбираются три сектора. Оперение расположено в плоскостях между областями. В каждой из областей применяется преобразование (4.1), которое обеспечивает нормировку расчетной области в радиальном направлении. Функции f₁, f₂, g во всех областях имеют одинаковое значение.

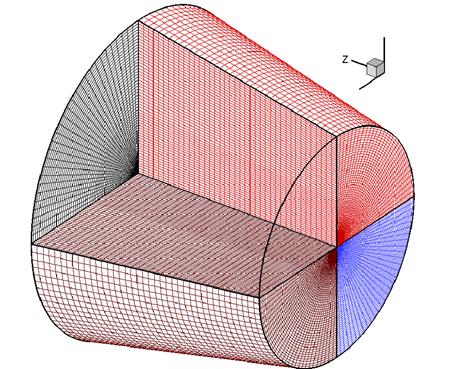
Рис.4.1

Для интегрирования системы (4.2) применяется схема МакКормака [9] аналогично, как и при расчете внешнего обтекания ракеты. Введение разностной сетки, разностные формулы, ограничение на шаг интегрирования приведены в подразделе 3.1.

Рассмотрим выполнение граничных условий. В предложенном разбиении расчетной области есть три типа границ (на рис.4.2 обозначены кружком):

1) граница, соответствующая поверхности сопла или канала контейнера;

2) граница, соответствующая оси сопла - канала;

3) граница между соседними областями;

На границе типа 1 должно быть выполнено условие непротекания. Схема удовлетворения данного условия приведена в подразделе 3.1.

На границе типа 2, соответствующей оси канала, расчетная сетка имеет особенность. Расчетная сетка в каждой области имеет по радиусу N узлов, а по j - M узлов, оси канала соответствуют узлы со значением индекса n = 1. Все M×k узлов (k - количество областей) при n = 1 совпадают. Значения газодинамических функций в этом случае получаются как среднее арифметическое значений газодинамических функций при n = 2 всех областей (при вычислении среднего арифметического учитывается направление вектора скорости).

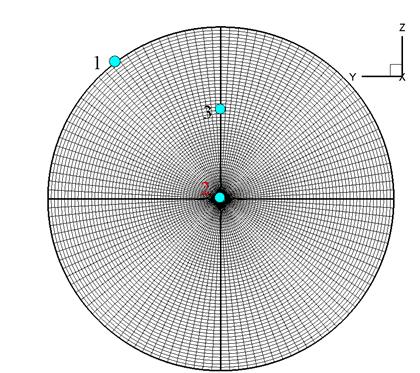
Рис.4.2

На границе типа 3 может быть расположено оперение – схема построения и удовлетворения граничных условий описана в подразделе 3.1.

В результате разработан достаточно простой метод расчета сверхзвукового течения внутри осесимметричного канала с учетом возможности расположения в потоке тонкого оперения. Метод основан на построении многообластной осесимметричной сетки и линеаризации граничных условий на поверхности оперения.