Шаг вывода на печать
Количество элементарных площадок для описания оперения
6. 0.5 8. 1.5 9. 1.5 0 0 0 0 0. x1, y1, x2, y2, x3, y3, d, j
6. 0.5 9. 1.5 9. 0.5 0 0 0 0 0.
Тип кривой, образующей тело
4. 0.5 0. 0. C1, C2, C3, C4 - константы
Конечное значение участка
10. 0.5 0. 0.
10.
───────────────────────────────────────────────
Начальное и конечное значения маршевой координаты определяют область интегрирования по продольной координате.
Характерные площадь и длина используются при расчете интегральных характеристик (единицы измерения должны соответствовать единицам, используемым при вводе геометрии тела).
Далее вводится геометрия оперения - количество элементарных площадок K для описания оперения. Затем вводится K наборов по 11 чисел. 6 чисел описывают элементарную площадку.
Необходимо пояснить, что такое элементарная площадка. Возможны различные способы описания геометрии оперения. Здесь использован следующий: оперение разбивается на набор треугольных площадок, для каждой из которых по всей их площади должны быть постоянны угол отклонения (для руля) и угол наклона образующей профиля. Если расчетная точка не принадлежит никакой элементарной площадке, то она расположена вне оперения, а если принадлежит, то таким образом определяются наличие оперения и соответствующие граничные условия. Для описания четырехугольного плоского крыла необходимо выделить 2 треугольные площадки, если крыло имеет ромбовидный профиль - 4; комбинация «плоский треугольный руль + четырехугольный плоский стабилизатор» - 3. Если учитывать сложный профиль и количество консолей - руль, дестабилизатор, крыло, стабилизатор, то потребное количество элементарных площадок может быть достаточно большим. Выбор за элементарную основу треугольных площадок продиктован геометрическими соображениями: треугольник всегда выпуклая фигура и на треугольники можно разбить произвольный многоугольник.
Шесть чисел – (x1, y1), (x2, y2), (x3, y3) - координаты вершин треугольника в плоскости (z, r). Для правильного выбора внутренней области треугольника последовательность вершин требуется вводить так, чтобы они были расположены по часовой стрелке.
Для каждой элементарной площадки вводятся углы поворота d (руля, в градусах) по количеству возможных плоскостей – в описываемом варианте программы 4; и угол наклона образующей профиля j (в градусах). Если угол поворота di по модулю больше некоторой условной величины (например, 40), то считается, что в данной плоскости элементарная площадка отсутствует. Это позволяет рассматривать варианты геометрии планера типа « ´ + » или варианты без наличия какой-либо лопасти.
Далее вводится геометрия корпуса. В отличие от оперения, геометрия корпуса вводится по мере продвижения по маршевой координате, т.е. сначала рассчитывается течение до некоторого заданного значения маршевой координаты и только затем в файле берется следующая часть информации.
Геометрия корпуса описывается образующей, которая состоит из набора различных кривых, в данной версии используется 4 типа кривых.
Кривая определяется значениями 6 параметров: k - тип кривой; c1, c2, c3, c4 – константы; конечное значение маршевой координаты для данного участка образующей:
k = 0 - образующая прямая, в этом случае прямая проводится из текущей точки в точку с координатами (с1, с2) (текущая точка - последняя точка предыдущего участка образующей, если первый участок имеет тип k = 0, то текущая - точка (0, 0) ). Таким образом, если тело образуется ломаной, то для описания его геометрии нужно будет ввести координаты изломов;
k = 1 - образующая эллипс. Уравнение эллипса в используемых константах имеет вид 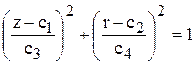 ;
;
k = 2 - образующая степенная функция. Уравнение данной функции в используемых константах имеет вид 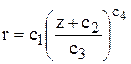 ;
;
k = 3 - образующая полином. Уравнение полинома в используемых константах имеет вид 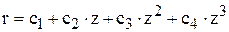 .
.
Данный набор функций может быть расширен посредством доработки подпрограммы расчета геометрии тела.
Геометрия корпуса должна быть описана вплоть до конечного сечения по маршевой координате и не должна содержать разрывов по радиусу. Есть еще одно дополнительное условие, заключающееся в том, что должно быть соответствие между наклоном образующей в начальном сечении Z (вычисляемым при вводе геометрии тела) и углом полураствора конуса, используемым при получении начального газодинамического поля.
На рис.3.83 приведена геометрия планера в соответствии с представленными данными.
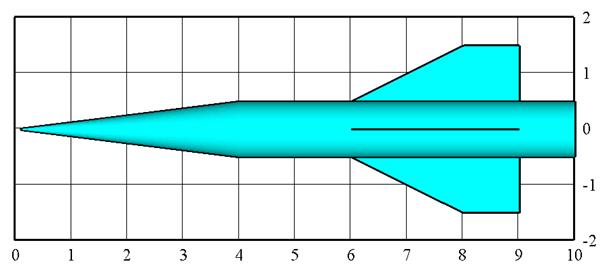
Рис.3.83
Этим заканчивается описание исходной информации для расчета по программе HHKK.EXE. По возможности исключены все параметры, которые касаются метода расчета, оставлено лишь то, что описывает геометрию и внешний поток в максимально коротком виде. Выполнение программы заключается в выполнении трех команд
При выполнении программы HHKK.EXE формируются текстовые файлы с результатами расчета, которые содержат интегральные аэродинамические характеристики в зависимости от маршевой координаты и распределенные поля давления (и другие газодинамические функции). Для обработки данных файлов используются соответствующие программы анализа или программы, позволяющие представить информацию в графическом виде.
В табл.3.4 представлено время одного варианта расчета рассматриваемой геометрии при разных числах Маха, на различных сетках (реально применяемых при расчете) и нескольких типах компьютера.
Таблица 3.4
| № | Мах | Сетка | Компьютер | Время, с |
| 35*31*8 | AMD Athlon 64, 3.2 Ghz | |||
| 65*31*8 | AMD Athlon 64, 3.2 Ghz | |||
| 35*61*8 | AMD Athlon 64, 3.2 Ghz | |||
| 65*61*8 | AMD Athlon 64, 3.2 Ghz | |||
| 125*61*8 | AMD Athlon 64, 3.2 Ghz | |||
| 65*121*8 | AMD Athlon 64, 3.2 Ghz | |||
| 65*31*8 | AMD Athlon 64, 3.2 Ghz | |||
| 65*31*8 | AMD Athlon 64, 3.2 Ghz | |||
| 65*31*8 | AMD Athlon 64, 3.2 Ghz | |||
| 65*31*8 | Pentium 3, 0.5 Ghz | |||
| 65*31*8 | Pentium 4, 1.9 Ghz | |||
| 65*31*8 | Pentium 4, 2.4 Ghz | |||
| 65*31*8 | Pentium 4, 2.8 Ghz |
Число Маха определяет область течения (расстояние между узлами) и скорость распространения возмущений, что, в целом, определяет шаг интегрирования и соответственно время решения задачи.
Время решения задачи возростает с уменьшением числа Маха, это объясняется увеличением угла конуса Маха. Уменьшение расстояния между узлами по радиусу с ростом числа Маха мало влияет на шаг интегрирования, так как для тел большего удлинения определяющим становится расстояние между узлами в окружном направлении.
Время расчета варианта T в зависимости от количества узлов n должно иметь зависимость 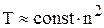 . Увеличение количества узлов в 2 раза должно приводить к повышению объема вычислений на шаге интегрирования в 2 раза. Кроме того, при этом шаг интегрирования должен уменьшаться в 2 раза (пропорционален расстоянию между узлами), что приводит к соответствующему увеличению числа шагов интегрирования. Данная зависимость выполняется не строго из-за различий по окружному и радиальному направлениям. Реально на современных персональных компьютерах можно проводить расчеты и с большим количеством узлов для более подробного, а следовательно, и более точного описания решения.
. Увеличение количества узлов в 2 раза должно приводить к повышению объема вычислений на шаге интегрирования в 2 раза. Кроме того, при этом шаг интегрирования должен уменьшаться в 2 раза (пропорционален расстоянию между узлами), что приводит к соответствующему увеличению числа шагов интегрирования. Данная зависимость выполняется не строго из-за различий по окружному и радиальному направлениям. Реально на современных персональных компьютерах можно проводить расчеты и с большим количеством узлов для более подробного, а следовательно, и более точного описания решения.
Возможность проведения варианта расчета с затратами времени порядка нескольких минут позволяет проводить систематические расчеты компоновок планеров. Обычный набор расчетов включает в себя не менее 3 вариантов геометрии планера (корпус без оперения, корпус с оперением с отклоненными и неотклоненными рулями при небольшом значении угла атаки). Расчеты проводятся для нескольких значений числа Маха, что позволяет построить основные аэродинамические характеристики в линейном приближении. Проведение расчетов при больших значениях углов атаки и отклонения рулей обычно связано со значительными сложностями, которые обусловлены принятой физической моделью течения (без отрыва и с сохранением сверхзвукового характера течения по продольной координате). Как правило, при больших углах атаки необходимо использование более сложной модели.
Глава 4
Дата добавления: 2016-09-06; просмотров: 2000;











