ТЕЧЕНИЕ В КАНАЛЕ БЕЗ ОПЕРЕНИЯ

В качестве теста были проведены расчеты течения в коническом сопле, результаты сравнивались с приближением одномерной теории течения газа. При задании в начальном сечении профиля скорости таковым, что в каждой точке вектор скорости направлен вдоль лучей из центра конического сопла, то течение в каждом сечении остается близким к однородному, а распределение газодинамических параметров вдоль оси сопла соответствует одномерной теории.

На рис.4.3 приведено сравнение давления по оси конического сопла: 1 - кривая соответствует одномерной теории; 2 – в начальном сечении задается поток параллельный оси сопла; маркерами 3 – в начальном сечении в соответствии с конической симметрией. В начальном сечении число Маха М = 3.

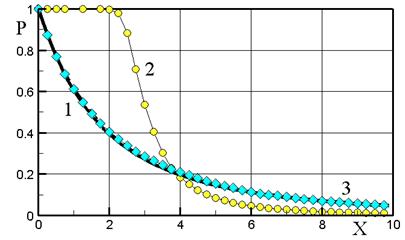
Рис.4.3

Видно, что в случае 2 течение не согласуется с одномерной теорией, так как при таком задании начальных условий поток в сопле становится существенно двумерным (рис.4.4). Соответствие одномерной теории и результата расчета (в случае задания начальных условий в соответствующем виде) позволяет сделать вывод о выполнении законов сохранения в реализованном разностном решении поставленной задачи.

Представить трехмерную картину течения можно в виде изолиний газодинамических параметров в некоторых сечениях или в виде изображений трехмерных поверхностей постоянного уровня той или иной газодинамической функции. Приведем несколько примеров трехмерного изображения. На рис.4.5 приведено осесимметричное течение в расширяющемся канале в виде трех поверхностей давления по уровням 0.9, 0.55 и 0.2. В начальном сечении М = 3, показатель адиабаты g = 1.4, вектор скорости направлен параллельно оси канала. Наклон стенки канала за начальным сечением характеризуется величиной tgj = 0.2 (j » 11.5^o), где j - угол наклона образующей канала. Отношение длины рассматриваемой части канала к диаметру начального сечения L/d = 2. Образуется течение разрежения относительно излома образующей канала (соответствует начальному сечению).

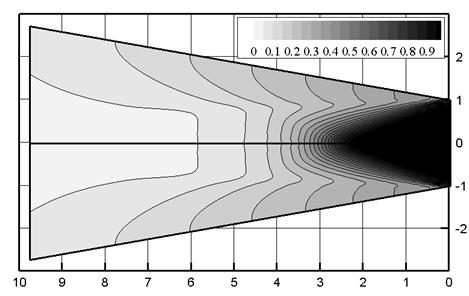
Рис.4.4

На рис.4.6 приведено то же самое течение, но в виде нескольких сечений по продольной координате и в плоскости, проходящей через ось канала.

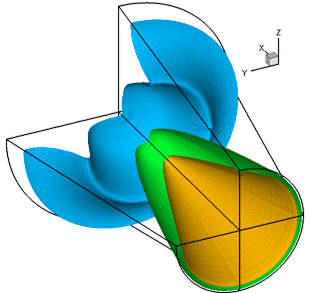
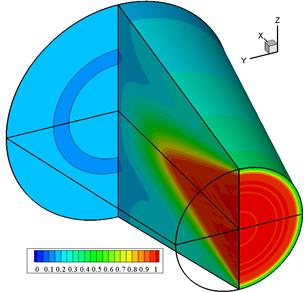
Рис.4.5 Рис.4.6

На рис.4.7, 4.8 представлено течение, образующее при сжатии, в аналогичном виде. В начальном сечении задаются параметры, соответствующие коническому течению из сопла, а канал далее становится цилиндрическим. При этом от точки излома образуется волна сжатия. На рис.4.7 поверхности построены по уровням давления 1.0, 1.5 и 2.

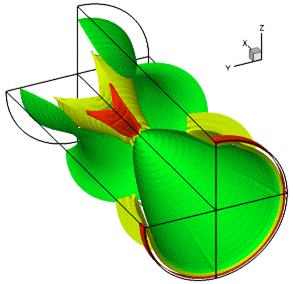
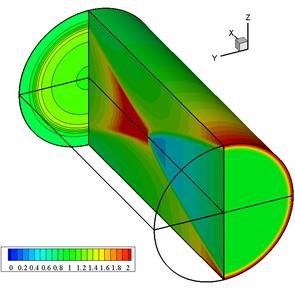
Рис.4.7 Рис.4.8

Канал состоит из расширяющегося сопла и длинной цилиндрической части, в которой образуется «периодическое» течение в виде волн сжатия. На рис.4.9, 4.10 приведено течение в относительно длинном канале L/d = 6. В данном случае видим образование трех зон повышенного давления, полученных с помощью ударных волн как на оси канала, так и на его стенках.

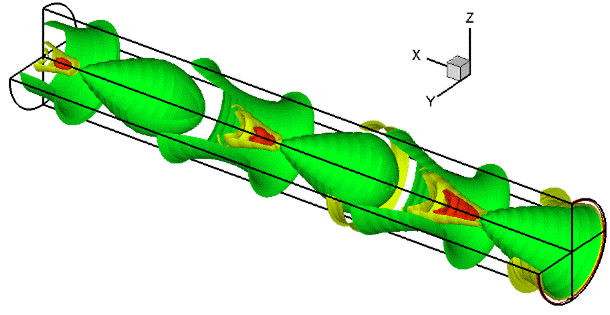
Рис.4.9

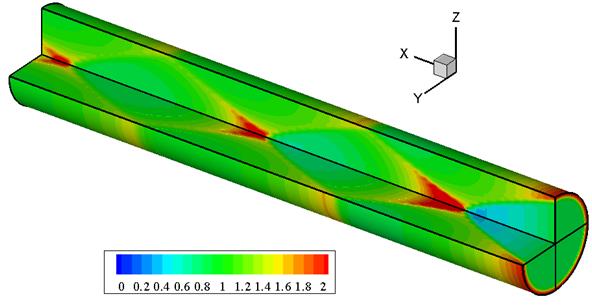
Рис.4.10