РАСЧЕТ ТЕЧЕНИЯ ОКОЛО ВРАЩАЮЩЕГОСЯ

ОПЕРЕННОГО ТЕЛА

Рассмотрим пример расчета вращающегося оперенного тела, экспериментально и теоретически исследованного в [9]. На рис.3.74 приведена геометрия планера: корпус – конус l = 1.86 + цилиндр l = 2.61; прямоугольное крыло - полный размах 2D, хорда 0.75D, где D - диаметр корпуса.

Рис.3.74

На рис.3.75 показан момент 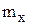в зависимости от безразмерной скорости вращения 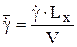при числе Маха М = 3, d = 5^о для случаев: 1 - a = 0^о, 2 - a = 10^о. В качестве характерной площади - мидель корпуса; характерного размера – радиус корпуса. Для рассматриваемой геометрии угол атаки незначительно влияет на момент крена.

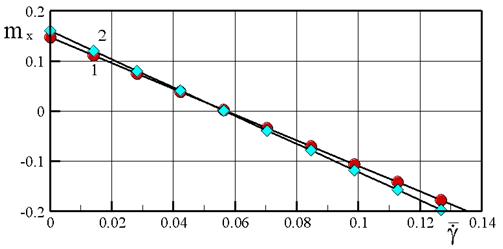
Рис.3.75

Прямой способ скорости авторотации предполагает расчет течения при наличии вращения с угловой скоростью 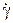с определением 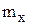. Надо подобрать значение 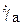такое, чтобы момент по крену был равен нулю: 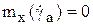. Фактически скорость авторотации определяется точкой пересечения функции с осью абсцисс (см. рис.3.75).

В ряде случаев скорость авторотации можно определить проще. Получив решение без вращения при заданном угле установки консолей d, находим коэффициенты момента по крену на консоль 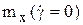и нормальной силы на консоль 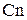. Центр давления на консоль по размаху определяется выражением: 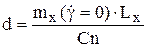. Скорость авторотации 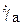приближенно вычисляяется из соотношения 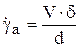, где V - скорость набегающего потока. Следовательно, безразмерная скорость авторотации

,

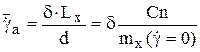где d - в радианах. Так может быть определена скорость авторотации без расчета течения с учетом вращения.

Если сделаны два расчета – без вращения и с некоторой скоростью вращения 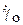, то из-за линейного изменения функции 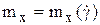имеем следующее выражение для нахождения скорости авторотации:

.

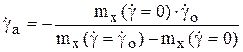На рис.3.76 приведена скорость авторотации рассматриваемой геометрии в зависимости от угла атаки, полученная на основе: расчета без вращения (1), двух расчетов (2), расчетов при разных значениях 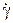(3). Результаты хорошо согласуются между собой и с экспериментальными данными [9].

Рис.3.76

На рис.3.77 - 3.79 приведены волны, индуцированные косо поставленным оперением d = 5^о: рис.3.77 – без вращения 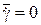; рис.3.78 – в режиме авторотации 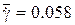; рис.3.79 – 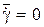.109. Течение представлено распределением Dp в сечении около задней кромки крыла. В представленном виде вращение направлено по часовой стрелке.

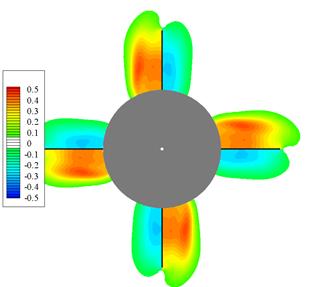
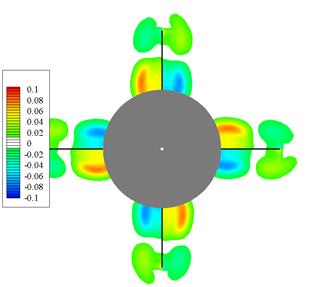
Рис.3.77 Рис.3.78

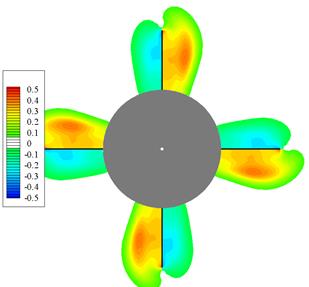
Рис.3.79

На примере планера представленного на рис.3.62, рассмотрим изменение скорости авторотации в зависимости от выбора рулевой поверхности.

На рис.3.80 приведена скорость авторотации в зависимости от угла атаки при М = 2 для четырех вариантов планера; аэродинамические поверхности, отклоненные для вращения по крену на угол d = 1^о, выделены темным цветом.

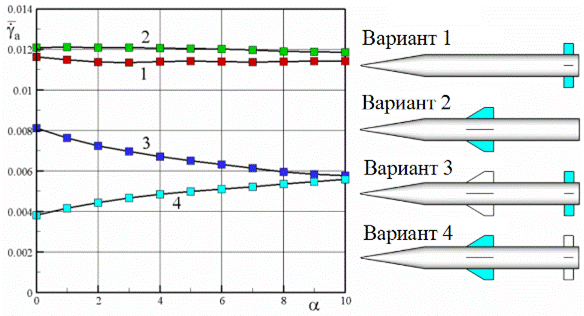
Рис.3.80

Скорость авторотации 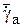варианта 2 по сравнению с вариантом 1 выше из-за смещения центра давления по радиусу к бортовой хорде. Скорость авторотации вариантов 3 и 4 меньше по причине дополнительной аэродинамической поверхности. Вариант 3 условно соответствует схеме «утка» (косо поставленное крыло расположено сзади). Скос потока при малых углах атаки от стоящего впереди руля приводит к увеличению 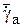. В варианте 4 (условно соответствующего нормальной аэродинамической схеме), наоборот, на малых углах атаки скос от косо поставленного крыла на руль приводит к уменьшению .

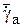Представляет интерес влияние отклонения руля на 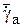. Для варианта 3 результаты представлены на рис.3.81, для варианта 4 – на рис.3.82.

Рис.3.81 Рис.3.82

В случае схемы «утка», при отклонении стоящего впереди руля на угол 5^о скорость авторотации существенно изменяется: линия 3а соответствует отклонению горизонтального руля, т.е. создающего подъемную силу в плоскости угла атаки; линии 3b и 3с - отклонению вертикального руля (в двух направлениях – влево и вправо), т.е. создающего боковую силу. В последнем случае из-за вращения ракеты отклонение руля в разных направлениях приводит к существенно разным результатам. Отклонение руля в скоростной системе координат достаточно условно из-за вращения. Пунктирной линией представлено среднеарифметическое значение 3b и 3c. Для схемы «утка» отклонение рулевых поверхностей может оказывать существенное влияние на момент по крену.

Отклонение руля в нормальной схеме мало влияет на скорость авторотации. Влияние руля проявляется только при его отклонении в вертикальной плоскости и больших углах атаки. Это связано с различиями условий обтекания лопастей руля, находящихся на наветренной и подветренной сторонах.