РАСЧЕТЫ ТЕЧЕНИЙ ОКОЛО ИЗОЛИРОВАННЫХ КОРПУСОВ

Приведем результаты расчетов течений около изолированных корпусов. Для оценки точности метода используется сравнение расчетных и экспериментальных результатов [44, 45, 46, 47] по суммарным АДХ компоновки «конус + цилиндр». Проведенные систематические расчеты (1.5 < М < 6, a до 20^о) позволили выделить область применения, в которой АДХ могут быть получены с точностью не менее 10 %.

Тело «конус + цилиндр» может быть описано двумя геометрическими параметрами: l_н - удлинением головной части или конуса (отношение длины головного конуса к диаметру корпуса), данный параметр связан с углом полураствора конуса соотношением l_н = [2tg(a_к)]^-1; l_ц - удлинением цилиндрической части (отношение цилиндрической части к диаметру корпуса). Полное удлинение корпуса l = l_н + l_ц.

На рис.3.4 приведено расчетное и экспериментальное изменение коэффициента нормальной силы Cn и момента тангжа m_z (определен относительно Xт = 0.66, характерная длина - полная длина корпуса) в зависимости от удлинения цилиндрической части. Параметры задачи: М = 3, a = 6 и 12^о, l_н = 5.9, l_ц = 0 ¸ 4. Для данных небольших удлинений цилиндрической части даже при относительно большом удлинении головной части есть соответствие расчетных и экспериментальных значений.

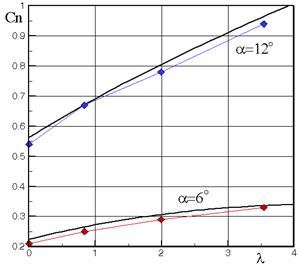
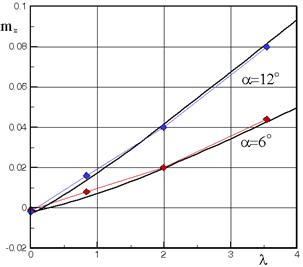
Рис.3.4

При проектировании ракетной техники интерес представляет наличие длинной цилиндрической части. На рис.3.5 приведено расчетное и экспериментальное изменение Cn и центра давления Xd в зависимости от удлинения цилиндрической части. Параметры задачи: М = 3.25; a = 6 и 10^о, l_н = 2.5, l_ц = 0 ¸ 22.

Для достаточно больших удлинений цилиндрической части (типичных для ракет) при a = 6^о расчет не соответствует эксперименту. Максимальная величина l_цил, при которой есть соответствие расчета и эксперимента, зависит от числа Маха и угла атаки.

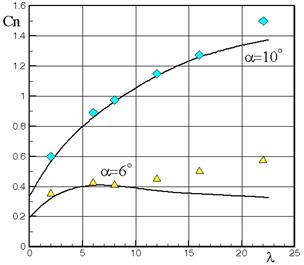
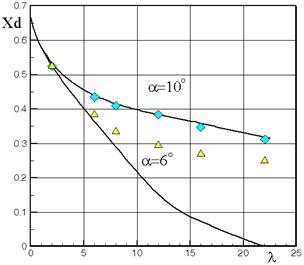
Рис.3.5

Расчет течения около корпусов большего удлинения рассматривался в ряде работ. Если суммировать полученные результаты, то получится следующее:

1) система уравнений Эйлера, т.е. расчет без учета вязкости, не позволяет описать течение с отрывом потока на подветренной стороне корпуса;

2) в ряде случаев, когда вклад в суммарные АДХ подветренной стороны мал, точный расчет течения на подветренной стороне не важен.

Известно, что на цилиндрических корпусах при удалении от головной части на расстояние, большее 6 ¸ 7 калибров, наблюдается равномерное распределение аэродинамической нагрузки по длине корпуса. Равномерное распределение нагрузки по кормовым частям цилиндрических корпусов обусловлено реализацией поперечного течения со скоростью V×sina. В соответствии с этим предположением представим коэффициент нормальной силы цилиндрической части в виде зависимости Cn_ц = sin²a×f(M×sina). Здесь коэффициент нормальной силы Cn_ц рассчитан относительно площади цилиндрической части в плане. Данная зависимость f(M×sina) получена в [1] и приведена на рис.3.6 (сплошной толстой линией - среднее значение, тонкими - границы экспериментального разброса). Обтекание кормовой цилиндрической части можно рассматривать независимо. Поперечное обтекание цилиндра определяется, кроме параметра M×sina, вязко-невязким взаимодействием, которое в используемой модели течения не учитывается. По этой причине ясно несоответствие расчета и эксперимента.

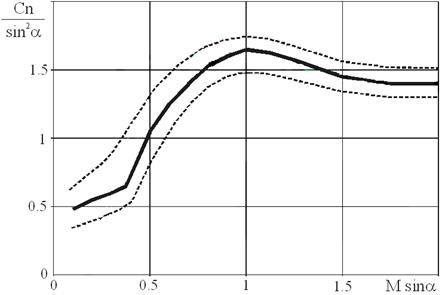
Рис.3.6

На рис.3.7 приведено расчетное и экспериментальное изменение Cn в зависимости от l_ц. Параметры: М = 4, a = 4, 6, 8^о, l_н = 2., l_ц = 0¸13. Маркерами представлены экспериментальные данные, разные маркеры соответствуют различным исследованиям. Видно соответствие расчета с одними экспериментальными результатами и отличие с другими для достаточно больших удлинений. Данный факт объясняется тем, что при проведении испытаний были реализованы различные режимы вязко-невязкого взаимодействия. При определении режима течения и интегральных характеристик важно учитывать вязкость потока.

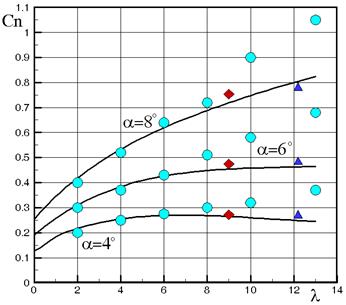
Рис.3.7

Оценим область применения физической модели в зависимости от параметра M×sina: отложив по оси абсцисс данный параметр, а по оси ординат l_ц, отметим предельные точки, для которых есть соответствие расчета и эксперимента. Через полученные таким образом точки (отмечены маркерами на рис.3.8) можно провести линию, ниже которой расчет и эксперимент находятся в соответствии.

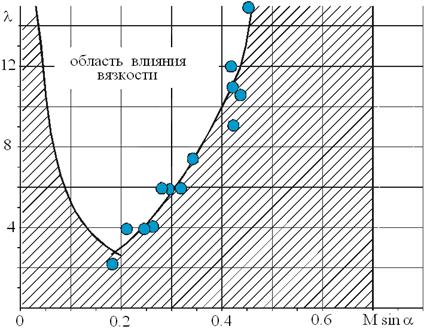
Рис.3.8

В данной области находятся точки, соответствующие не только малым удлинениям цилиндрической части, но и большим (l_ц > 6) при достаточно большом значении M×sina. Это не означает, что используемая физическая модель позволяет описать точно течение в данной области. Подъемная сила кормовой цилиндрической части формируется из двух составляющих: давления на наветренной стороне и давления на подветренной стороне. Давление на наветренной стороне формируется внешним невязким потоком, а давление на подветренной стороне является следствием вязко-невязкого взаимодействия. Эти составляющие подъемной силы в зависимости от параметров могут вносить различную долю. В тех случаях, когда вклад течения на подветренной стороне достаточно велик, используемая физическая модель не позволяет получить правильный результат. Данный факт отражен в ряде работ положением: по мере роста числа Маха точный расчет течения на подветренной стороне не всегда необходим при определении интегральных характеристик. Действительно, с ростом числа Маха область применения модели невязкого газа становится шире (в более широком диапазоне удлинений корпуса).

В расчете при M×sina > 0.7 возникают проблемы вычислительного характера: как и при расчете течения около конуса. При больших углах атаки на подветренной стороне корпуса образуются поперечные ударные волны, которые приводят к колебаниям давления за границу физически реальных значений. Реализованная программа не позволяет проводить расчеты при M M×sina > 0.7, её следует признать границей области расчета.

При малых значениях параметра M×sina < 0.3 трудно сопоставить расчет и эксперимент в связи с малым изменением Cn при изменении длины цилиндрической части. Подъемная сила представляется в виде

,

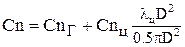где Cn_Г, Cn_Ц - подъемная сила головного конуса (может быть рассчитана) и цилиндрической части, D - диаметр корпуса.

Так как Cn_Ц < 0.6×sina при M×sina < 0.3 и приближенно Cn_Г > 0.04a (a - в градусах), для того чтобы ошибка в определении Cn составила не более 5 %, необходимо выполнение соотношения: 0.05×0.04×a > 0.6×sin²a×l_ц× 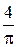, или приближенно 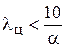(a -в градусах).

Данная зависимость приведена на рис.3.8 (при М = 3). Реальная граница области применимости с ошибкой менее 5 % лежит выше, так как на части цилиндра оценка подъемной силы делается правильно.

Практически после проведения расчета АДХ около тел большего удлинения делается уточнение вклада цилиндрической части в соответствии с зависимостью, приведенной на рис.3.6, что позволяет получить соответствие в достаточно широком диапазоне параметров (M, a).

В [1] при рекомендуемой оценке подъемной силы цилиндрической части корпуса также предполагается, что на цилиндрической части реализуется только положительная подъемная сила. Это выражается в росте значения подъемной силы с увеличением параметра удлинения цилиндрической части. На рис.3.9 приведено сравнение расчетной оценки и рекомендуемой в [1] величины Cn^a корпуса «конус + цилиндр» в зависимости от параметра .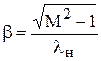

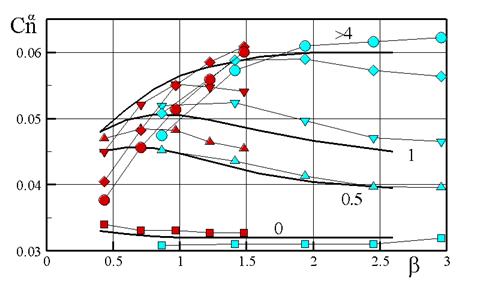
Рис.3.9

Линиями приведены данные [1]. Расчетные данные отмечены маркерами и получены при М = 2, 3, 4, 5, 6; l_н = 2, 4; a = 1^о. Приведены результаты при значении параметра 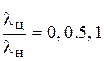и . При 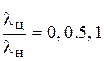расчеты и данные [1] хорошо согласуются. Оценка [1] максимального значения Cn^a корпуса «конус + цилиндр» является огибающей расчетных данных.

Кроме определения суммарных АДХ можно рассчитать локальные газодинамические параметры, например, давление. На рис.3.10 приведено сравнение экспериментального (маркерами) и расчетного распределений давления при М = 2.; a = 3, 6, 10^о и М = 3.; a = 10^о на наветренной и подветренной сторонах тела «степенное оживало + цилиндр» l_н = 2.5, l_ц = 2.5. Головная часть выполнена в виде степенного оживала: .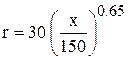

М = 2, a = 3^о М = 2, a = 6^о

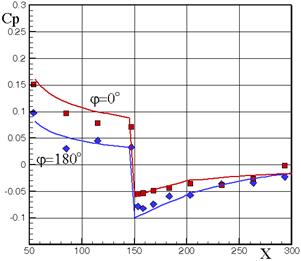
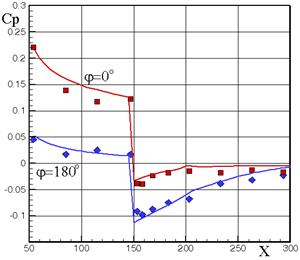
М = 2, a = 10^о М = 3, a = 10^о

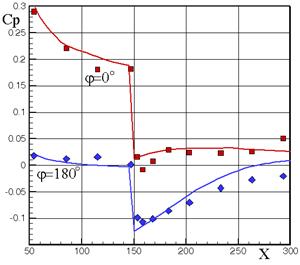
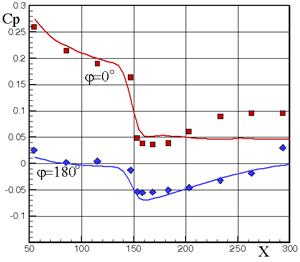
Рис.3.10

На рис.3.11 представлено сравнение с экспериментальным распределением давления на наветренной и подветренной сторонах тела «конус (7.05^о) + цилиндр +конус (10^о)» при М = 4.; a = 10^о.

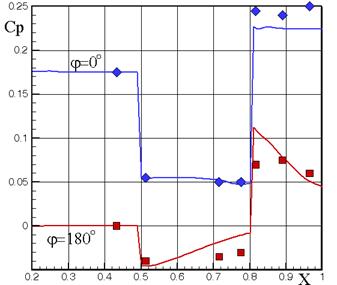
Рис.3.11

По результатам расчета получается большой объем информации в виде трехмерных полей газодинамических параметров. Большое значение имеет графическое отображение информации, что позволяет контролировать правильность задания геометрических параметров, дает возможность представить результаты в максимально обобщенном виде, выявить характерные особенности течения.

Вид сбоку