Основные законы аэродинамики
Уравнение неразрывности.
Уравнение неразрывности струи воздушного потока (постоянства расхода ) - это уравнение аэродинамики, вытекающее из основных законов физики - сохранения массы и инерции. Устанавливает связь между плотностью, скоростью и площадью поперечного сечения струи воздушного потока.
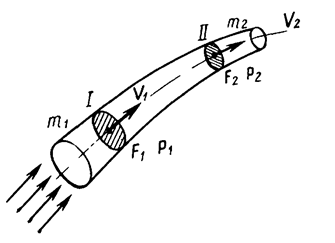
Рис. 2.5 Пояснение к закону неразрывности струи воздушного потока
Уравнение сформулировано Л. Эйлером в 1756г. применительно к движению струйки жидкости.
В струйке переменного сечения через сечение I за одну секунду протекает некоторый объем воздуха (рис.2.5). Этот объем равен произведению скорости воздушного потока V на площадь поперечного сечения F.
Секундный массовый расход воздуха в струйке mc равен произведению секундного объема на плотность ρ воздушного потока.
Согласно закону сохранения материи масса жидкости (воздуха) в струйке m1, протекающей через сечение I, должна быть равна массе m1, протекающей через сечение II, при условии, если движение воздушного потока установившееся:
m1=m2=cons,  ρ1 F1V1= ρ2 F2V2=const.
ρ1 F1V1= ρ2 F2V2=const.
Для любого сечения струйки можно записать:
ρFV=const.
Это выражение называется уравнением неразрывности (постоянства расхода) для струйки воздушного потока.
При малых скоростях движения воздух ведет себя как несжимаемая жидкость. Поэтому плотность воздуха в любом сечении струйки одинакова r1=r2=const.
Для несжимаемой жидкости уравнение можно записать в следующем виде: F1V1=F2V2= const или в виде пропорции:
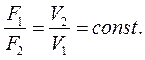
Из формулы видно, что для любого сечения скорость воздушного потока струи обратно пропорциональна площади ее поперечного сечения и наоборот:
V= 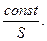
Вывод: Уравнение неразрывности устанавливает взаимосвязь между сечением струи и скоростью при условии, что воздушный поток струи установившийся.
Задача. Определить скорость течения потока жидкости V2 в узком сечении трубки площадью S2=5см2,если через широкое сечение трубки площадью S1=7,5см2 скорость течения составляет V1=20м/с.
Решение: V2/V1=S1/S2. V2=V1S1/S2=20*7,5/5=30м/с.
Закон Бернулли.
Основные явления, происходящие при течении газа и жидкости, можно объяснить, применяя к движущейся среде закон сохранения энергии.
Выделим струйку в потоке несжимаемого газа и проведем в ней два поперечных сечения 1 и 2 (см. рис.2.5). Этими поперечными сечениями определится объем газа, к которому мы применим закон сохранения энергии. При этом будем считать, что движение газа установившееся.
Пусть за единицу времени через сечение 1 проходит масса газа m1. В этом месте струйки газ имеет скорость V1, а давление p1. За то же время через другое сечение 2 струйки , где скорость газа равна V2, а давление p2, вытекает такая же масса газа m2.
При установившемся течении в выделенной части струйки не происходит ни накапливания, ни расхода энергии, т.к. между струйкой и окружающей её средой обмен энергией отсутствует.
Следовательно, энергия, передаваемая газу за единицу времени через сечение 1, должна быть равна энергии, передаваемой за то же время через сечение 2.
Согласно закону сохранения энергии, полная энергия струйки воздушного потока в различных сечениях есть сумма нескольких видов энергии потока: кинетической, потенциальной энергии сил статического давления, внутренней энергии и энергии положения. Эта сумма должна быть величиной постоянной:
Екин+Ер+Евн+Еп=сопst .
Кинетическая энергия Екин - способность движущегося воздушного потока совершать работу под действием сил динамического давления;
Потенциальная энергия Ер - способность воздушного потока совершать работу под действием сил статического давления;
Внутренняя энергия Евн - это способность газа совершать работу при изменении его температуры;
Энергия положения Eп - способность воздуха совершать работу при изменении положения центра тяжести данной массы воздуха при подъеме на определенную высоту.
Таким образом, газ, находящийся позади сечений 1 и 2, производит работу по продвижению впереди лежащей массы газа. Эта работа производится силами давлений статического и динамического (скоростного напора).
При движении несжимаемого идеального газа сумма статического и динамического давлений остается величиной постоянной. Эта сумма называется полным напором.
Рассмотрим течение жидкости (газа) через трубу переменного диаметра (Рис.2.6). Анализируя показания манометров, можно сделать заключение, что наименьшее давление показывает манометр сечения 3-3.
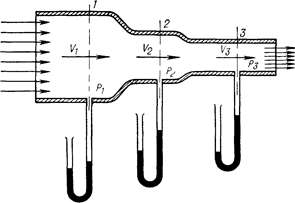
Рис. 2.6 Объяснение закона Бернулли
Причиной падения давления является то, что воздушный поток не производит никакой работы, поэтому полная энергия воздушного потока остается постоянной. Если считать температуру, плотность и объем воздушного потока в различных сечениях постоянными, то внутреннюю энергию можно не рассматривать.
Значит, возможен переход кинетической энергии воздушного потока в потенциальную и наоборот.
Когда скорость воздушного потока увеличивается, то увеличивается скоростной напор и кинетическая энергия данного воздушного потока. Статическое давление при этом уменьшается.
Преобразуем уравнение сохранения полной энергии: для сечений 1,2,3:
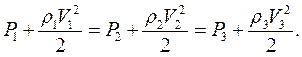
где: P- статическое давление; 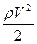 - скоростной напор.
- скоростной напор.
Для любого сечения струйки воздуха уравнение можно записать в следующем виде:
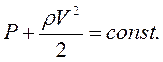
В таком виде записывается уравнение Бернулли.
Оно показывает, что сумма статического и динамического давлений для любого сечения струйки установившегося несжимаемого воздушного потока есть величина постоянная.
Уравнение Бернулли широко применяется в практических условиях. Этот закон используется при конструировании приборов для измерения скорости движения жидкости и газов, различного рода инжекторов, водоструйных насосов, карбюраторов, при изучении причины образования подъемной силы крыла.
Принцип работы указателя скорости летательного аппарата показан на рис.2.7.
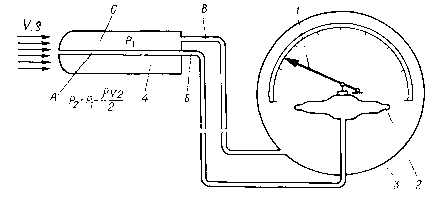
Рис. 2.7 Измерение скорости воздушного потока
Вывод: Законы аэродинамики являются теоретической основой для изучения процессов обтекания крыла и летательного аппарата, способов расчета аэродинамических сил.
Аэродинамический эксперимент. Для подтверждения теоретических расчетов выполняются практические исследования в специальных аэродинамических лабораториях.
Аэродинамическиеэксперименты проводятся в аэродинамических трубах – установках, в которых можно создать искусственный регулируемый поток воздуха или газа. Аэродинамические исследования проводятся в аэродинамических трубах малых скоростей, трубах больших дозвуковых скоростей, трубах сверхзвуковых скоростей, трубах специального назначения (штопорных, дымовых) и т.д.
Первая аэродинамическая труба в России была построена основоположником современной ракетной техники К.Э. Циолковским в 1887 г. в г. Калуге.
Простейшая схема аэродинамической трубы прямого действия показана на рис.2.8. Труба состоит из коллектора (суживающегося сопла), рабочей части, диффузора и вентилятора.
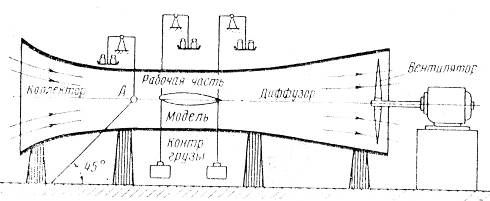
Рис. 2.8 Аэродинамическая труба прямого действия
Вентилятор, приводимый во вращение электродвигателем, создает в трубе поток воздуха. Назначением диффузора является плавное уменьшение скорости при входе к вентилятору, чтобы снизить потери на трение воздуха о стенки трубы.
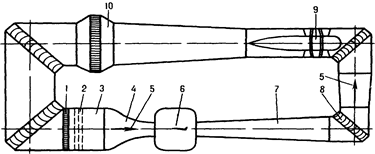 Основным отличием трубы замкнутого типа от трубы прямого действия является наличие обратного канала, создающего для воздуха замкнутый путь. На рис. 2.9 приведена схема аэродинамической трубы замкнутого типа с открытой рабочей частью.
Основным отличием трубы замкнутого типа от трубы прямого действия является наличие обратного канала, создающего для воздуха замкнутый путь. На рис. 2.9 приведена схема аэродинамической трубы замкнутого типа с открытой рабочей частью.
Рис. 2.9 Аэродинамическая труба замкнутого типа
Поток воздуха, обтекающий модель в рабочей части трубы, подается в диффузор. Пройдя через диффузор, воздух через поворотные колена и обратный канал поступает в наиболее широкую часть трубы, называемую форкамерой.
В форкамере установлена спрямляющая решетка, пройдя через которую воздух поступает в суживающееся сопло. Это сопло обеспечивает нужную скорость потока в рабочей части трубы. Для уменьшения завихрения потока воздуха во всех поворотных коленах установлены специальные профилированные лопатки.
Для измерения аэродинамических сил и моментов, действующих на модель в воздушном потоке, применяются аэродинамические весы (см. рис.2.8). В основу устройства аэродинамических весов положен принцип уравновешивания модели при нарушении ее положения равновесия под действием возникающих аэродинамических сил и моментов. Для того, чтобы привести модель в исходное положение равновесия, необходимо нагрузить чашки весов или рычаги.
Передача усилий от модели к весовым рычагам может быть механической, электромеханической или гидравлической. В настоящее время широкое распространение получили аэродинамические весы тензометрического типа. На весах этого типа при помощи тензометров измеряются упругие деформации весовых элементов, размещаемых внутри моделей, а затем по деформациям определяются аэродинамические силы и моменты.
Занятие №4
Дата добавления: 2016-09-06; просмотров: 19007;











