РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ С ОДНИМ ИСТОЧНИКОМ

Схемы электрических цепей.Главной задачей расчета электрической цепи является определение токов отдель­ных элементов цепи (источников, приемников, прибо­ров и др.)- Определив значение тока, легко найти напря­жение, мощность. Значения этих величин необходимы для того, чтобы правильно выбрать или оценить условия работы элементов цепи, путем сравнения рабочих величин с номинальными. Расчеты проводят по схемам элект­рических цепей.

Схема электрической цепи—это графиче­ское изображение, содержащее, условные обозначения элементов электрической цепи и показывающее соеди­нения между ними. Различают принципиальные схемы, схемы соединений и схемы замещения.

Принципиальные схемы, на которых в виде условных обозначений представлен полный состав элементов цепи и связи между ними, позволяют получить детальное представление о работе электроустановки при ее из­учении.

На схемах соединений (монтажных), по которым осуществляется монтаж электроустановок, показаны ме­ста соединения составных частей установки, точки при­соединения и ввода проводов, жгутов, кабелей.

Если в принципиальной схеме опустить элементы, которые не влияют на расчет цепи (приборы, предохра­нители, выключатели и др.), а остальные заместить (за­менить) их сопротивлениями R и ЭДС £, получим схему замещения, используемую при расчетах.

Наиболее общим случаем цепи с одним источником является цепь со смешанным соединением сопротивле­ний (см. рис. 2.11, 2.16). Расчет этих цепей основывается на использовании закономерностей последовательного и параллельного соединения сопротивлений.

Последовательное соединение сопротивлений.При по­следовательном соединении элементов цепи конец первого элемента присоединяется к началу второго, конец вто­рого — к началу третьего ит. д. В результате образуется неразветвленная ветвь цепи, на всех участках которой, в соответствии с положением (3) , один и тот же ток.

К двум узлам схемы на рис. 2.11 (узел — это место соединения ветвей) присоединены четыре ветви.

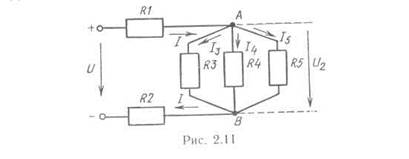
В одной из них соединены последовательно источник и сопротив­ления R₁ и R₂. Соединение сопротивлений R₁ и R₅ нельзя назвать последовательным, так как через них проходят разные токи.

По второму закону Кирхгофа U = U₁+U₂+U₃,

U = IR₁ + IR₂ + IR₃ ; (2.19)

I= U/(R₁ + R₂ + R₃) = U/R, (2.20)

где R— общее сопротивление цепи:

R =R₁ + R₂ + R₃ (2.21)

Таким образом, при последовательном соединении сопротивлений: 1) на всех элементах один и тот же ток; 2) общее (эквивалентное) сопротивление ветви равно сумме сопротивлений ее элементов; 3) общее напряжение ветви, распределяясь на элементах прямо пропорцио­нально их сопротивлениям, равно сумме напряжений

участков ветви (1).

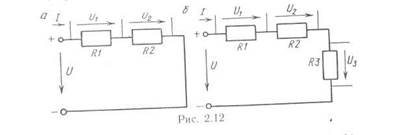
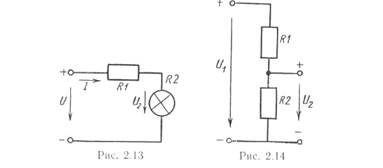
На практике при необходимости уменьшить напряже­ние и ток приемника последовательно ему подключают резистор (2). Например, лампочка карманного фонарика, рассчитанная на ток 0,2А, и имеющая R = 20 Ом, при прямом включении в сеть 220 В перегорит, так как ток I = U/R = 220/20 = 11А значительно превышает допу­стимый ток 0,2А. Если же последовательно лампочке включить резистор R = 1200 Ом (рис. 2.13), то I= U/(R₁ +R₂) = 0,18А, что допустимо. При этом напря­жение на лампочке уменьшается

до U₂ = IR ₂=0,18 • 20 = 3,6В (при напряжении источника 220 В).

Иногда уменьшение напряжения осуществляется по схеме делителя напряжения (рис. 2.14). В этой схеме сопротивления резисторов R₁ и R₂ можно подобрать так, чтобы получилось на выходе нужное напряжение U₂.

Применение последовательного соединения элементов ограничено его недостатками: при выходе из работы одного элемента нарушается работа других элементов ветви, и при изменении сопротивления одного из элемен­тов изменяются ток и напряжения на других элементах. Параллельное соединение сопротивлений.При парал­лельном соединении элементов цепи все они присоеди­нены к одной паре узлов, т. е. находятся под действием одного и того же напряжения.

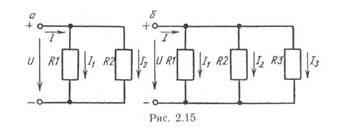
Из закона Ома следует, что при параллельном соеди­нении приемников ток и напряжение каждого из них не зависят от числа приемников, если напряжение источ­ника неизменное. При этом включение и отключение одного из приемников не влияет на работу других. Поэто­му параллельное соединение элементов нашло широкое применение на практике.

В соответствии с балансом мощностей:

Р = Р₁+Р₂ + Р₃;

UI = UI₁ + UI₂ + UI₃;

I = I₁ + I₂ + I₃ . (2.22)

С другой стороны, используя выражение (2.11), по­лучаем:

P ₌ P₁ + P₂ + P_3;

U ²g = U² g₁+ U² g₂ +U²g₃ (2.23)

g = g₁ + g₂ + g ₃ ,

где g — общая проводимость всей цепи.

Таким образом, при параллельном соединении сопро­тивлений:

1) напряжения на всех сопротивлениях оди­наковые;

2) общая (эквивалентная) проводимость цепи равна сумме проводимостей параллельных ветвей;

3) общий ток цепи равен сумме токов ветвей (3).

Используя уравнения (2.9) и (2.23), получаем вы­ражение для расчета эквивалентного сопротивления цепи.

1/R = 1/R₁ + 1/R₂+ 1/R₃. (2.24)

При параллельном соединении двух сопротивлений

R = R₁R₂ /(R₁+R₂).

При параллельном соединении п одинаковых сопро­тивлений

R = R₁ /n.

Уравнение (2.22) представляет собой частный случай первого закона Кирхгофа: сумма токов, направ­ленных к узлу электрической цепи, равна сумме токов, направленных от узла.

При расчете цепей со смешанным соединением сопро­тивлений применяют метод преобразования (свертыва­ния) схем. Сущность метода заключается в замене отдель­ных групп последовательно или параллельно соединен­ных сопротивлений эквивалентными сопротивлениями.