Лекция 20. Взаимодействие электронов и позитронов с веществом

20.1. Особенности взаимодействия быстрых электронов с веществом.При прохождении через вещество быстрых электронов и позитронов (в т.ч. β-частиц, испускаемых радионуклидами) главным механизмом потерь энергии, как и для тяжелых заряженных частиц, являются ионизация и возбуждение атомов. Однако характер торможения электронов отличается от характера торможения тяжелых частиц. Во-первых, из-за малой массы электрона рассеяние на большие углы оказывается настолько существенным, что после некоторого числа столкновений электрон «теряет память» о первоначальном направлении своего движения. По этой причине понятие пробега электрона теряет изначальный смысл. Учитывая запутанность траектории движения электрона, следует различать средний путь, пройденный электроном в среде, и среднее удаление его (по прямой) от точки входа в среду (рис. 20.1).

Вторая особенность, также обусловленная малой массой электрона, состоит в том, что к ионизационному торможению добавляется другой весьма важный механизм – радиационное торможение. В соответствии с законами электродинамики при торможении заряженной частицы в электромагнитном поле должно испускаться тормозное излучение, интенсивность которого обратно пропорциональна квадрату ускорения а:

.

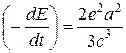Ускорение заряженной частицы, которое она испытывает в кулоновском поле другой частицы с зарядом Ze, обратно пропорционально ее массе m_a:

.

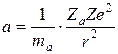Тогда

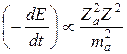. (20.1)

Отсюда следует, что превышение радиационного торможения электронов над радиационным торможением, например, α-частиц определяется фактором (M_α/Z_αm_e)², т.е. составляет более чем 6 порядков.

Наконец, в-третьих, при расчете тормозной способности вещества по отношению к быстрым электронам следует учитывать релятивистские эффекты. Энергия покоя электрона равна 0,511 МэВ; кинетическая энергия β-частиц, испускаемых большинством радионуклидов – величина того же порядка. Таким образом, пренебречь релятивистскими эффектами, как в случае α-частиц, уже нельзя.

Взаимодействие электронов с атомными ядрами при всех энергиях имеет исключительно электромагнитный характер (если, конечно, пренебречь слабым взаимодействием) и сводится, в основном, к упругому рассеянию.[166] В сильных взаимодействиях электроны не участвуют.

20.2. Ионизационное торможение электронов.При однократном рассеянии электронов друг на друге они могут терять значительную часть своей энергии (в среднем половину). Если считать, что первичный электрон всегда обладает большей энергией, чем электрон отдачи, его потери при однократном соударении в среднем составят одну четвертую часть. Расчеты потерь энергии электрона на единице длины пути были проведены Бете. В наиболее общей форме эти потери определяются следующей формулой:

,

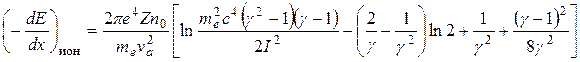где γ = E/E₀ – отношение полной энергии электрона к его энергии покоя, а смысл остальных обозначений – тот же, что в формуле (19.8). Можно показать, что в классическом пределе (g ® 1)

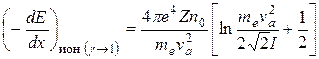. (20.2)

Отличие этого выражения от (19.6) обусловлено, главным образом, тождественностью сталкивающихся частиц (электронов). Результатом неразличимости частиц в квантовой механике является не имеющий классического аналога обменный эффект, несколько снижающий тормозную способность.[167] Этот эффект становится существенным при малых скоростях налетающего электрона, когда его кинетическая энергия сравнима с энергией связи атомных электронов.

В ультрарелятивистском пределе (v_a » c, g ® ¥)

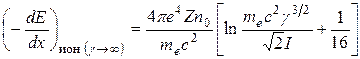. (20.3)

Как и в случае тяжелых частиц, неограниченному росту ионизационных потерь препятствует эффект плотности. Чтобы учесть его, в формулу (20.3) следует ввести поправку, учитывающую поляризацию среды.

Флуктуации потерь энергии электронов существенно больше, чем для тяжелых заряженных частиц, что связано с большим диапазоном энергии, которую может потерять электрон при одном соударении. Энергетические спектры электронов после прохождения через слои вещества разной толщины показаны на рис. 20.2. Конечно, это распределение обусловлено не только флуктуациями в потерях энергии: не меньшее значение имеют и многократные упругие соударения. Но и в том случае, если исключить влияние многократного рассеяния, разброс потерь энергии на определенном участке трека оказывается большим. В связи с этим потери энергии электрона на единице длины его пути имеют смысл только средних величин.

20.3. Радиационное торможение.При очень больших энергиях электроны начинают более эффективно терять ее из-за преобладания радиационного механизма торможения с испусканием тормозного излучения. Хорошо известным примером тормозного излучения нерелятивистских электронов является излучение антикатода рентгеновской трубки (п. 1.2). Согласно соотношению (20.1), при столкновении электрона с ядром интенсивность тормозного излучения растет пропорционально квадрату заряда ядра. В то же время при столкновении с электронами атома интенсивность растет пропорционально их числу, т.е. Z. Поэтому в веществах с большими атомными номерами радиационные потери обусловлены, в основном, торможением ядрами.

Полное рассмотрение радиационного торможения в рамках теории, которая носит название квантовой электродинамики,[168] было выполнено Бете и В. Гайтлером. Даже в случае взаимодействия электрона с «голым» ядром эта теория дает весьма сложное выражение для радиационных потерь. Результат существенно упрощается лишь в предельных случаях:

,

,

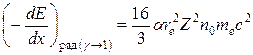где α = e²/ħc – постоянная тонкой структуры (1/a » 137), r_e = e²/m_ec² – классический радиус электрона, n₀ – плотность атомов вещества.

При еще более точных расчетах необходимо принять во внимание эффект экранирования: при прохождении через вещество электрон взаимодействует не с «голым» ядром, а с ядром, окруженным электронами. С учетом этого эффекта

. (20.4)

Радиационные потери релятивистского электрона прямо пропорциональны его полной энергии (так как E = m_ec²γ):

.

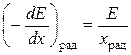Иными словами, при прохождении через вещество быстрый электрон теряет свою энергию на расстояниях порядка

.

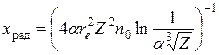Расстояние х_рад называется радиационной длиной. Другая эквивалентная характеристика радиационного торможения – радиационная толщина – связана с радиационной длиной через плотность вещества:

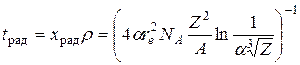, (20.5)

где N_A – число Авогадро. В связи с тем, что Z/A ≈ const, радиационная толщина падает при переходе от легких веществ к тяжелым практически обратно пропорционально Z. Она изменяется от 85 г/см² для He до 5,8 г/см² для Pb.

Тормозное излучение имеет непрерывный спектр, верхняя граница которого определяется кинетической энергией электронов T_e. Энергетическая зависимость спектра при больших значениях T_e передается законом n(E_γ) ~ 1/E_γ, где E_γ – энергия, теряемая электроном при испускании одного кванта тормозного излучения. Поэтому потери энергии на испускание тормозного излучения не зависят от E_γ: в любой части тормозного спектра электрон теряет примерно одинаковую энергию. Эта энергия может быть потеряна при испускании одного жесткого кванта, уносящую всю энергию dE, теряемую на данном пути dx, или нескольких мягких квантов с той же суммарной энергией. Энергетическое распределение интенсивности излучения, испускаемого при торможении электронов в тонкой мишени, дано на рис. 20.3. В случае толстой мишени, размеры которой больше нескольких радиационных длин, спектр будет другим. Чтобы его получить, необходимо усреднить приведенные спектры, принимая во внимание ионизационные потери и зависимость радиационных потерь от энергии.

Угловое распределение тормозного излучения имеет ярко выраженную направленность: большинство фотонов тормозного излучения рентгеновской трубки испускаются в направлении, перпендикулярном направлению движения электронов. При релятивистских энергиях электронов тормозное излучение испускается преимущественно вперед; средний угол вылета фотона равен 1/γ.

Отметим, что радиационные потери пропорциональны Z². В связи с этим для защиты от быстрых электронов целесообразно использовать материалы с малым атомным номером (алюминий, оргстекло и т.п.), так как в противном случае увеличивается выход тормозного излучения, проникающая способность у которого гораздо выше, чем у самих электронов.

20.4. Сопоставление потерь энергии. Таким образом, при прохождении через вещество быстрых электронов независимо друг от друга работают два механизма торможения – ионизационный и радиационный:

.

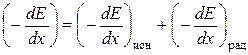Характер зависимости ионизационных и радиационных потерь от энергии электрона и от параметров среды различен, поэтому различно и соотношение вкладов этих двух механизмов (рис. 20.4). При небольших энергиях (вплоть до десятка МэВ) преобладают ионизационные потери, так как

.

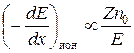При более высоких энергиях, т.е. уже в релятивистской области, ионизационные потери практически перестают зависеть от энергии, а радиационные прямо пропорциональны ей:

; .

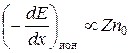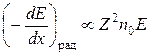Численные оценки показывают, что справедливо следующее приближенное равенство:

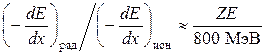. (20.6)

Для количественной характеристики перехода от режима доминирования ионизационного торможения над радиационным к противоположному вводится понятие критической энергии электрона Е_кр, при которой, по определению, эти вклады равны:

.

Нетрудно видеть, что даже для такого тяжелого элемента, как свинец (Z = 82) радиационные потери начинают преобладать над ионизационными при Е порядка 10 МэВ. В среднем на пути, равном радиационной длине, электрон с энергией выше Е_кр испускает один фотон с энергией, сравнимой с его собственной энергией, и несколько фотонов с гораздо меньшей энергией.

20.5. Взаимодействие позитронов с веществом.Взаимодействие с веществом электронов и позитронов имеет много общего. В частности, для позитронов оказываются справедливыми практически все предыдущие рассуждения относительно ионизационных и радиационных потерь энергии. Действительно, массы электрона и позитрона и их заряды по абсолютной величине равны (вспомним, что заряд проходящей через вещество частицы входит в формулы только в виде четных степеней). Некоторое отличие связано с тем, что в системе электрон-позитрон не возникает обменного эффекта: это все-таки разные частицы! В результате для позитронов

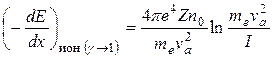, (20.7)

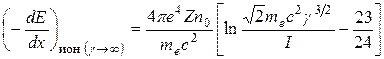. (20.8)

Различие в поведении электронов и позитронов проявляется, главным образом, на самых последних стадиях замедления и связано с аннигиляцией позитронов с электронами вещества

,

с образованием нескольких γ-квантов. Один γ-квант испуститься не может, так как это противоречит закону сохранения импульса (ПРИЛОЖЕНИЕ К).

Сечение аннигиляции растет с уменьшением энергии позитрона: в связи с этим аннигиляция почти всегда происходит лишь после замедления позитрона до тепловых энергий. Оно зависит также от относительной ориентации спинов электрона и позитрона. Аннигиляция в синглетном состоянии, когда спины антипараллельны (суммарный спин системы S = 0), в ~1100 раз более вероятна, чем в триплетномсостоянии, когда спины параллельны (S = 1). В синглетном состоянии обычно образуется два γ-кванта (двухфотонная аннигиляция) с энергией m_ec² = 0,511 МэВ, в триплетном – три (трехфотонная аннигиляция).[169] Среднее время жизни позитронов относительно аннигиляции зависит от электронной плотности вещества.

При встрече замедленного позитрона с атомным электроном (до того, как произошла аннигиляция) возможно образование промежуточной связанной системы – атома позитрония. Различают ортопозитроний (S = 1; среднее время жизни τ – около 1,4·10^–7 с) и парапозитроний (S = 0, τ ≈ 1,25·10^–10 с). Потенциал ионизации позитрония I_Ps = 6,8 эВ (вдвое меньше, чем у атома водорода).[170]

Не все позитроны аннигилируют в составе позитрония: он образуется лишь в течение ~20% времени замедления позитрона; в остальное время позитроны аннигилируют в столкновениях как свободные частицы. Это объясняется тем, что образование позитрония может произойти только тогда, когда кинетическая энергия позитрона больше, чем разность I – I_Ps, где I – потенциал ионизации атома (молекулы) вещества. Однако, если энергия существенно превышает эту минимальную величину (достигая, например, I), то соударение с большой вероятностью приведет просто к ионизации.

20.6. Пробег монохроматических электронов и β-частиц.Пробег электронов в веществе можно исследовать путем анализа кривых поглощения N(x). Следует, однако, помнить, что многократное рассеяние на большие углы приводит к тому, что большинство частиц, испытав столкновение, выбывает из пучка, и только небольшая часть электронов проходит в поглотителе максимальное расстояние R_max в направлении их первоначального движения. В результате кривая поглощения монохроматических электронов выглядит так, как это изображено на рис. 20.5. Если линейный участок кривой экстраполировать к оси абсцисс, то такое экстраполированное значение пробега R_э может, как и R_max, служить мерой кинетической энергии электрона.

Для оценки максимального пробега электронов с энергией Е пользуются эмпирическими формулами. Например, экстраполированного пробега электронов в алюминии (это вещество принимают за стандарт) рекомендованы формулы:

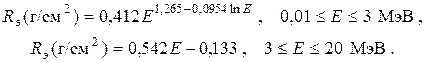(20.9)

В связи с тем, что радиационные потери не оказывают большого влияния на пробег (даже для ультрарелятивистских электронов они значительны только в самом начале торможения), пересчет пробега электронов на другие среды производится следующим образом:

. (20.10)

Максимальный пробег монохроматических электронов определяется экспериментально со значительной погрешностью, поэтому для практических целей используется редко.

Электроны и позитроны, образующиеся при распаде радионуклидов, имеют непрерывный энергетический спектр[171] с максимальной энергией Е_b и средней энергией » 0,33Е_b (п. 8.4). Максимальный пробег β-частиц, очевидно, совпадает с максимальным пробегом монохроматических электронов с энергией Е_b. Однако кривая поглощения пучка β-частиц, изображенная на рис. 20.5, по своему виду отличается от кривой поглощения монохроматических электронов. Это обусловлено тем, что β-частицы с низкими энергиями, выбывают из пучка гораздо раньше. В результате значительная часть кривой поглощения β-излучения (до ~0,7R_э) с достаточной точностью описывается экспоненциальной зависимостью:[172]

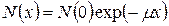, (20.11)

где х – толщина поглотителя (г/см²), m – массовый коэффициент поглощения β-частиц (см²/г), практически не зависящий от вещества и связанный с энергией Е_b (МэВ) эмпирической зависимостью:

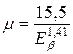(E_β > 0,5 МэВ). (20.12)

Массовый коэффициент поглощения β-частиц может, таким образом, использоваться для определения верхней границы β-спектра.

20.7. Черенковское излучение.Законы сохранения энергии и импульса запрещают частице, движущейся равномерно и прямолинейно в вакууме, отдавать свою энергию и импульс в виде электромагнитного излучения без изменения ее внутреннего состояния (ПРИЛОЖЕНИЕ К). Однако этот запрет снимается при движении частицы в среде с показателем преломления n > 1.

Представим для начала заряженную частицу, медленно движущуюся в среде. Вызываемая ее электрическим полем поляризация атомов среды[173] будет распределена симметрично относительно местонахождения частицы, так как распространяющееся со скоростью света электрическое поле «успевает» поляризовать все атомы вокруг, в том числе и находящиеся прямо на пути частицы (рис. 20.6-а). Результирующее поле образовавшихся диполей будет равно нулю, и испускаемые ими электромагнитные волны погасят друг друга.

Если же скорость частицы vв среде превышает скорость распространения в ней света (электромагнитных волн), т.е. v_a > c/n, то имеет место эффект запаздывания поляризации, в результате которого диполи будут получать преимущественную ориентацию в направлении движения частицы (рис. 20.6-б). В этом случае, очевидно, существует такое направление, вдоль которого может возникнуть когерентное излучение диполей, так как волны, испущенные ими, могут оказаться в одинаковой фазе. Это излучение быстрых заряженных частиц было открыто в 1934 г. П.А. Черенковым и С.И. Вавиловым и известно как черенковское излучение.

Направление распространения черенковского излучения легко найти, если воспользоваться принципом Гюйгенса для построения фронта излучаемой волны и построить огибающую (коническую) поверхность к сферическим волнам, испущенным частицей на пути из точки О в точку А. (рис. 20.7). Раствор конуса, вдоль образующих которого распространяется черенковское излучение, определяется соотношением

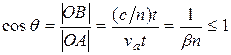. (20.13)

Он тем больше, чем больше скорость частицы. При минимальном для данной среды (пороговом) значении скорости, когда β = 1/n, т.е. когда еще возможно возникновение излучения, этот конус вырождается в узкий луч вдоль направления движения частицы. Для воды (n = 1,33) это условие эквивалентно равенству β = 0,75. Отсюда, в частности, следует, что электроны с энергией T_e ≥ 0,26 МэВ способны генерировать в воде черенковское излучение.

Потери энергии частицы с зарядом Z_a на черенковское излучение

, (20.14)

где интегрирование ведется по всему спектру частот ω электромагнитного излучения. Если забыть, что входящий в (20.14) показатель преломления среды зависит от частоты, может показаться, что спектр черенковского излучения (определяющийся множителем в скобках) является равномерным, и основные потери энергии приходятся на область высоких частот. В действительности в дальней ультрафиолетовой и рентгеновской области, где n < 1, черенковское излучение вообще отсутствует; его спектр оканчивается со стороны высоких частот в области ближнего ультрафиолета. Равномерность спектра в видимом диапазоне выражается в том, что интенсивность его высокочастотного (сине-фиолетового) края существенно выше, чем интенсивность низкочастотного (красного) края. Отсюда характерный голубоватый цвет черенковского излучения. Потери энергии на черенковское излучение составляют малую долю от общих потерь быстрых электронов.

В заключение подчеркнем, что черенковское излучение не имеет ничего общего с фактически всегда имеющим место тормозным излучением. Черенковское излучение испускается средой под влиянием поля движущейся в ней частицы, тормозное – самими частицами при их столкновениях с атомами. Различие между обоими типами излучений особенно ясно проявляется при переходе к пределу сколь угодно большой массы частицы: тормозное излучение при этом полностью исчезает, а черенковское не меняется вообще.

Лекция 21. Взаимодействие γ-квантов с веществом

21.1. Общие замечания.Процесс взаимодействия фотонного излучения с веществом с передачей ему энергии нельзя считать непрерывным, как это имеет место в случае тяжелых заряженных частиц. При прохождении через вещество фотон в единичном акте электромагнитного взаимодействия с атомом теряет всю свою энергию (поглощение) или значительную ее часть (рассеяние); в последнем случае фотон существенно изменяет и направление своего движения. Поэтому, в отличие от заряженных частиц, для фотонов не существует понятия пробега или потерь энергии на единицу длины пути.

Известно множество различных видов взаимодействия электромагнитного излучения с атомами. Однако, если только не считать ядерных реакций, уже рассматривавшихся в п. 17.4, основными видами взаимодействия с веществом для фотонов высокой энергии (вне зависимости от происхождения: γ-кванты, рентгеновское излучение и т.п.) являются фотоэффект, эффект Комптона и образование электрон-позитронных пар.

21.2. Фотоэффект. Фотоэффект, или фотоэлектрическое поглощение – это вырывание связанных атомных электронов под действием электромагнитного излучения.[174] Энергия γ-кванта Е_g передается электрону, который переходит из связанного состояния в свободное:

g + А ® А⁺ + e^- .

Фотоэффект невозможен на свободных (не связанных) электронах, так как для выполнения закона сохранения импульса, кроме фотона и электрона, необходимо присутствие третьего тела – атомного ядра (ПРИЛОЖЕНИЕ К).

Вероятность фотоэффекта тем больше, чем ближе энергия падающего кванта к энергии связи электрона. Поэтому фотоэлектрическое поглощение γ-квантов чаще всего происходит при взаимодействии с электроном одной из внутренних оболочек атома. С точностью до энергии отдачи иона А⁺, которая мала даже в случае легких атомов, кинетическая энергия фотоэлектрона определяется как

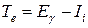, (21.1)

где I_i – энергия связи электрона на i-й атомной оболочке. Очевидно, что при Е_g < I_i фотоэффект невозможен. Освободившееся на электронной оболочке место заполняется одним из электронов с вышерасположенных оболочек. Этот процесс сопровождается испусканием характеристического рентгеновского излучения и электронов Оже, возникающих при разрядке возбужденных состояний атома (последнее с большей вероятностью наблюдается при фотоэффекте на атомах с малыми и средними значениями атомного номера Z).

Ввиду того, что масса ядра значительно больше массы электрона, бóльшая часть импульса γ-кванта передается ядру. Вероятность передачи импульса электрону зависит от энергии связи электрона с ядром и энергии γ-кванта. Именно этими обстоятельствами и обусловлены основные характеристики фотоэффекта в области высоких энергий: 1) зависимость сечения от энергии; 2) зависимость сечения от заряда ядра вещества-поглотителя; 3) соотношение вероятностей фотоэффекта на разных электронных оболочках.

Формулы для сечения фотоэффекта были получены методами квантовой электродинамики. Сечение фотоэффекта для атома водорода или для легкого водородоподобного иона с зарядом ядра Z определяется следующим выражением:

,

где a – постоянная тонкой структуры, r_e – классический радиус электрона,

(β_e – скорость фотоэлектрона в единицах c). Можно заметить, что вероятность фотоэффекта сильно зависит от заряда ядра (~ Z⁵), так как с ростом Z резко увеличивается энергия связи внутренних электронов с ядром (кулоновское взаимодействие). В нерелятивистском случае, когда I_i << Е_g << m_ec²

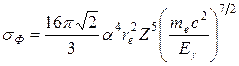. (21.2)

В ультрарелятивистском случае, когда ,

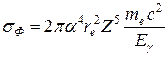. (21.3)

Полное сечение фотоэффекта для многоэлектронных атомов может быть вычислено только приблизительно с использованием численных методов. Однако при этом пропорциональность σ_Ф ~ Z⁵ и асимптотики σ_Ф(Е_g) в пределе малых и больших энергий фотона остаются справедливыми. Если проследить, как выглядит зависимость сечения фотоэффекта на многоэлектронном атоме по мере увеличения Е_g, то можно видеть две основные особенности: наличие резких краев поглощения на пороге ионизации I_i каждой оболочки и очень быстрый спад сечения по мере увеличения энергии после каждого из значений Е_g = I_i (рис. 21.1). Сочетание этих двух особенностей создает характерную пилообразную форму зависимости сечения от энергии.

Вероятность фотоэффекта на L-, M- и других оболочках значительно меньше, чем на К-оболочке: при энергиях γ-квантов, превышающих энергию связи на K-оболочке, s_L/s_K ≈ 1/5, s_M/s_L ≈ 1/4. Вероятность фотоэффекта на внешних оболочках крайне мала.

21.3. Эффект Комптона. При прохождении g-квантов через вещество, наряду с поглощением, происходит их рассеяние с изменением или же без видимого изменения длины волны. Рассеяние без изменения длины волны характерно для сравнительно мягкого рентгеновского излучения (Е_g << m_ec²). Оно называется классическим, или томсоновским и находит свое объяснение в рамках классической электродинамики: падающая на атом электромагнитная волна приводит в вынужденные колебания связанные электроны, которые сами становятся излучателями волн с той же частотой (длиной волны). Для сечения классического рассеяния Дж. Дж. Томсон получил следующую формулу:

. (21.4)

Рассеяние с изменением длины волны имеет место в тех случаях, когда энергия фотона сравнима с m_ec². Впервые это явление наблюдал А. Комптон (1922 г.) при исследовании рассеяния жестких рентгеновских лучей. В опытах Комптона было показано, что спектр рассеянного излучения, помимо первоначальной линии с длиной волны 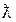, содержит смещенную линию 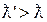, причем величина смещения растет с увеличением угла рассеяния θ, а при фиксированном θ не зависит ни от 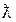, ни от вида рассеивающего вещества. Все эти закономерности не объясняются классической волновой теорией, зато находят объяснение с точки зрения квантовой теории. Комптон и Дебай предложили трактовать наблюдаемое явление как упругое рассеяние квантов света (фотонов) на электронах вещества (ПРИЛОЖЕНИЕ Л). В каждом отдельном акте взаимодействуют один фотон и один электрон; электрон в этом случае можно считать свободным, так как энергия падающих фотонов выше, чем энергия связи электронов в атомах.[175]

Полное сечение, определяющее число g-квантов, выбывших из первичного пучка (в расчете на один электрон), дается формулой Клейна-Нишины-Тамма:

, (21.5)

где x = 2E_γ/m_ec². Рассмотрим ее предельные случаи.

При x << 1 (нерелятивистский случай) число рассеянных g-квантов линейно убывает с ростом энергии g-квантов

.

В обратном, ультрарелятивистском случае (x >> 1)

.

Таким образом, сечение комптоновского рассеяния уменьшается с ростом энергии фотона; в пределе E_g ® ¥ практически обратно пропорционально E_g (рис. 21.1). Полное сечение рассеяния γ-квантов на атоме пропорционально числу электронов, т.е. .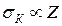

Энергетический спектр электронов отдачи (комптоновских электронов) непрерывен: их кинетическая энергия T_e распределена в интервале от 0 до максимальной величины, определяемой формулой Л.8 (ПРИЛОЖЕНИЕ Л).

Указанный на рис. 21.1 ход кривой, изображающей зависимость s_К от Е_g, относится к случаю бесконечно узкого пучка и точечного детектора, когда рассеянные на небольшой угол g-кванты не регистрируются. Однако на опыте употребляются пучки с конечным углом раствора, а детектор не является точечным. Поэтому весьма важно знание углового распределения рассеянных g-квантов.

При малых значениях x угловое распределение следует закону (1 + cos²φ), характерному для классической электромагнитной теории (φ – угол рассеяния γ-кванта). Это распределение симметрично относительно φ = π/2. Вероятность рассеяния максимальна при φ = 0^о и 180^о. С увеличением x угловое распределение становится все более и более направленным вперед. Кривые рис. 21.2 иллюстрируют характер углового распределения рассеянного g-излучения для различных значений Е_g. При x >> 1 практически все рассеянное излучение можно считать сосредоточенным в узком конусе с углом раствора φ = 2/x.

В некоторых случаях необходимо учитывать скорости электронов, взаимодействующих с фотонами. Движение атомных электронов приводит к заметному разбросу энергий рассеянных фотонов и электронов отдачи (при фиксированном θ). В частности, если импульс электрона больше импульса летящего ему навстречу фотона, то последний не теряет, а приобретает энергию (обратный эффект Комптона).

Кроме электронов эффект Комптона может происходить и на других заряженных (а также нейтральных, но имеющих ненулевой магнитный момент) частицах, например на протоне или нейтроне. Однако сечения рассеяния при этом очень малы, так как обратно пропорциональны квадрату массы частицы.

В заключение обсуждения комптоновского рассеяния g-квантов отметим, что с этим явлением связано не только их рассеяние, но и последующее фотоэлектрическое поглощение в веществе. Если источник g-квантов со всех сторон окружить достаточно большими блоками из легкого вещества (например, алюминия), то за пределы блоков g-излучение уже не выйдет. Это будет не так, если бы имело место классическое рассеяние. Однако при комптоновском рассеянии часть энергии g-кванта передается электрону. Поэтому в результате многократного рассеяния в блоке g-квант постепенно потеряет большую часть своей энергии, и, в конце концов, поглотится, так как сечение фотоэффекта быстро растет с уменьшением энергии и становится больше, чем сечение рассеяния (рис. 21.1). На явлении многократного рассеяния основано устройство защиты от g-квантов из бетона, кирпича и т.д.

21.4. Образование электрон-позитронных пар. При энергиях g-квантов, превышающих 2m_ec² (1,022 МэВ), наблюдается процесс поглощения g-квантов с образованием пары электрон-позитрон:

g + а ® e^– + e⁺ + а .

Энергия g-кванта тратится на создание этих двух частиц и на сообщение им кинетической энергии; таким образом, образование пары – эндотермический процесс. Исходя из законов сохранения энергии и импульса, можно показать, что образование пары в вакууме невозможно (ПРИЛОЖЕНИЕ К). Это может происходить только при взаимодействии g-излучения с другими частицами. В результате образования пары энергия и импульс должны распределиться между электроном, позитроном и какой-то третьей частицей (ядром или электроном), в поле которой образовалась пара. Если применить к процессу образования пары анализ, изложенный в п. 11.2, станет ясно, что при образовании пары в поле ядра пороговая энергия фотона равна 2m_ec², а в поле электрона 4m_ec².[176]

Оценим энергию отдачи при рождении пары в поле ядра. Максимальная отдача будет наблюдаться в том случае, если электрон и позитрон вылетают под углами 90^о относительно направления движения γ-кванта, причем угол их разлета равен 180^о. В этом случае импульс ядра отдачи равен импульсу γ-кванта, и для энергии отдачи справедлива формула (9.6). Отсюда получаем, что для Е_g = 10 МэВ при атомной массе вещества А > 10 энергия ядер отдачи не превышает 5 кэВ (т.е. менее 0,05%). Тогда сумма кинетических энергий электрона и позитрона с хорошей точностью равна

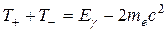. (21.6)

При относительно малых величинах Е_g эта энергия распределяется почти равновероятно между электроном и позитроном. С ростом Е_g преобладающим становится асимметричное распределение. Спектры электронов и позитронов несколько различаются, если принять во внимание, что при удалении от ядра, в поле которого образовалась пара, электроны испытывают торможение, а позитроны ускорение. Этот эффект тем больше, чем выше заряд ядра Z и чем меньше Е_g. Испускание электрона и позитрона при больших энергиях γ-кванта происходит в направлении движения последнего в пределах угла θ ≈ m_ec²/ Е_g. При малых энергиях угловое распределение менее анизотропно и зависит от Z.

Чем сильнее электрическое поле частицы, с которой взаимодействует γ-квант, тем вероятнее образование пар. Для сечения образования пары в поле «голого» ядра квантовая электродинамика дает следующее выражение:

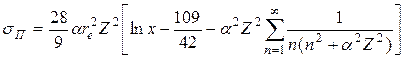. (21.7)

Для легких атомов (aZ << 1) σ_П ~ Z². Учет экранирования ядра атомными электронами приводит к тому, что в пределе E_g ® ¥ сечение процесса практически перестает зависеть от E_g. Энергетическая зависимость сечения образования пар показана на рис. 21.1.

При малых энергиях и больших Z сечение образования пары в поле электрона примерно в 10³ раз меньше. Однако при Е_g > 10 МэВ оно составляет около 1% общего сечения в тяжелых элементах и около 10% в легких. Энергия отдачи, получаемая атомным электроном, в этом случае того же порядка, что и кинетическая энергия частиц пары.

Образование электрон-позитронных пар в сочетании с радиационным торможением является причиной возникновения электрон-фотонных ливней в космических лучах (п. 18.6). Если фотон тормозного излучения имеет энергию Е_g >> m_ec², он может образовать пару, электрон и позитрон которой при торможении снова создают фотоны, и т.д. Процесс нарастает лавинообразно до тех пор, пока не будет достигнута критическая энергия (п. 20.4).

В широком диапазоне энергий γ-квантов суммарное сечение их взаимодействия с веществом s_Σ складывается из сечений трех основных процессов – фотоэффекта, эффекта Комптона и образования пар:

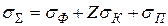. (21.8)

Из характера зависимости каждого из этих сечений от энергии γ-квантов следует, что в области малых энергий основным механизмом взаимодействия является фотоэффект, в промежуточной области – эффект Комптона,[177] а в области высоких энергий – образование электрон-позитронных пар. Значения энергии, отделяющие области преобладания каждого из трех эффектов, различны для разных сред. Сечение σ_Σ имеет минимум в области, где наиболее велико влияние комптоновского рассеяния (рис. 21.1). Этот минимум особенно резко выражен для тяжелых элементов.

21.5. Коэффициент ослабления. Экспоненциальный закон поглощения γ-квантов.Итак, при прохождении через вещество g-излуч