Лекция 19. Взаимодействие тяжелых заряженных частиц с веществом
19.1. Основные понятия и определения. К тяжелым заряженным частицам (масса которых много больше массы электрона) относятся протоны, α-частицы, более тяжелые ионы, осколки деления, мюоны, заряженные пионы и т.д. При прохождении через вещество тяжелых заряженных частиц возможно их упругое и неупругое рассеяние на ядрах, а также ядерные реакции. Однако главным механизмом взаимодействия является ионизационное торможение, при котором энергия частицы расходуется либо на выбивание электрона из оболочки атома (ионизация), либо на перевод электрона с одного энергетического уровня на другой (возбуждение). Оба процесса происходят вследствие кулоновского взаимодействия заряженной частицы с атомными электронами. При этом часть атомных электронов приобретает значительную энергию (т.н. δ-электроны) и вызывает вторичную ионизацию. На долю вторичной ионизации приходится 60-80 % от полной ионизации, т.е. от общего числа образовавшихся ионов.
Путь, пройденный частицей в веществе до ее полного торможения, называется пробегом, а число пар ионов nх, образовавшихся на единице длины пути, – удельной ионизацией. Потеря энергии частицей на единице пути называется удельной потерей энергии, или тормозной способностью вещества и обозначается как  . Величина
. Величина
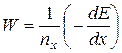 (19.1)
(19.1)
характеризует среднюю энергию, затрачиваемую на образование одной пары ионов. Установлено, что величина W практически не зависит от вида и энергии заряженной частицы и составляет единицы эВ в плотных средах. Для газов эта величина значительно больше и примерно в 2-3 раза превышает величину первого потенциала ионизации. Так, для воздуха W = 33,85 эВ, а первые потенциалы ионизации молекул О2 и N2 равны 12,07 и 15,58 эВ соответственно. Траектории движения заряженных частиц можно наблюдать в трековых детекторах (камерах Вильсона, пузырьковых или искровых камерах, ядерных фотоэмульсиях), регистрирующих удельную ионизацию.[162] Образующиеся в результате ионизации вторичные электроны, тормозясь в веществе, также оставляют следы в трековой камере. Максимальная энергия, передаваемая электрону тяжелой частицей, движущейся со скоростью va, приблизительно равна 2meva2 (ПРИЛОЖЕНИЕ И). Пользуясь соотношением масс электрона и α-частицы, нетрудно показать, что для α-частиц с энергией порядка нескольких МэВ эта величина достигает нескольких кэВ. Поэтому вдоль следа быстрой тяжелой частицы, густо усеянного ионами, появляются отростки с малой удельной ионизацией, обусловленные d-электронами. Экспериментальную информацию о прохождении заряженных частиц через вещество дают кривые Брэгга, показывающие, как распределена удельная ионизация, производимая частицей, по траектории ее движения. Типичная кривая Брэгга для тяжелой частицы представлена на рис. 19.1. В начале движения, пока частица еще не потеряла своей скорости, удельная ионизация невелика и медленно и монотонно растет по мере замедления. К концу пробега удельная ионизация увеличивается до некоторого максимального значения, а затем довольно быстро спадает до нуля. Уменьшение удельной ионизации в конце пути связано с захватом электронов и многократной перезарядкой частиц. Так, например, α-частица (4Не2+) в некоторых столкновениях захватывает атомный электрон и часть своего пути совершает уже в виде однозарядного иона 4Не+, для которого, как будет показано ниже, удельная ионизация примерно в четыре раза меньше. Однозарядный ион может потерять электрон, а может и захватить еще один электрон, превратившись в нейтральный атом 4Не. Эффект перезарядки заметно возрастает при уменьшении скорости частицы и особенно важен для многозарядных осколочных ядер.

 19.2. Классическая теория ионизационного торможения.Классическаятеория торможения тяжелых заряженных частиц основывается на представлении о том, что проходящая через вещество частица взаимодействует с атомными электронами как с независимыми свободными частицами. При этом потери энергии частицей за счет ее взаимодействия с отдельными электронами просто суммируются в предположении равномерного распределения электронов в веществе. Предполагается также, что потери энергии частицы при столкновении с одним электроном настолько малы, что искривление ее траектории ничтожно: частица движется прямолинейно (о чем свидетельствуют треки в камере Вильсона и т.д.) и равномерно. Кроме того, частица пролетает мимо электрона настолько быстро, что последний не успевает изменить своего положения в пространстве за время столкновения.
19.2. Классическая теория ионизационного торможения.Классическаятеория торможения тяжелых заряженных частиц основывается на представлении о том, что проходящая через вещество частица взаимодействует с атомными электронами как с независимыми свободными частицами. При этом потери энергии частицей за счет ее взаимодействия с отдельными электронами просто суммируются в предположении равномерного распределения электронов в веществе. Предполагается также, что потери энергии частицы при столкновении с одним электроном настолько малы, что искривление ее траектории ничтожно: частица движется прямолинейно (о чем свидетельствуют треки в камере Вильсона и т.д.) и равномерно. Кроме того, частица пролетает мимо электрона настолько быстро, что последний не успевает изменить своего положения в пространстве за время столкновения.
Рассмотрим взаимодействие быстрой (но нерелятивистской) тяжелой заряженной частицы, несущей заряд Za, с одним из электронов вещества. Пусть частица пролетает мимо него с постоянной скоростью va по прямолинейной траектории с прицельным параметром b (рис. 19.2). Разложим кулоновскую силу
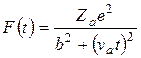 ,
,
действующую в каждый момент времени t со стороны частицы на электрон, на продольную и поперечную составляющие F||(t) и F^(t). Согласно сформулированным выше допущениям продольный импульс силы òF||(t)dt, полученный за время t < 0, полностью компенсируется импульсом силы, полученным за время t > 0. Поперечный же импульс силы оказывается равным
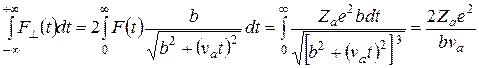 . (19.2)
. (19.2)
Приравняв его к импульсу (количеству движения) электрона pe, вычислим кинетическую энергию электрона после его взаимодействия с пролетевшей частицей:
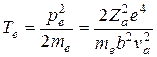 . (19.3)
. (19.3)
Такова потеря энергии частицы при взаимодействии с одним электроном, отстоящим от траектории ее движения на расстоянии b. Далее, пусть частица проходит слой вещества dх. Вырежем в нем мысленно тонкий кольцевой цилиндр, так чтобы его ось совпадала с траекторией движения частицы. Число электронов в этом кольцевом цилиндре равно
 ,
,
где ne – плотность атомных электронов в веществе. Потери энергии частицы за счет взаимодействия с этими электронами составляют TedNe. Чтобы получить всю величину потерь энергии частицы при прохождении слоя dх, необходимо проинтегрировать (19.3) по плоскости, в которой лежит этот слой вещества:
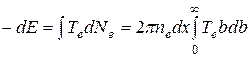 .
.
Отсюда для тормозной способности вещества получаем
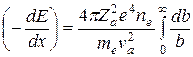 . (19.4)
. (19.4)
Стоящий в правой части выражения (19.4) интеграл логарифмически расходится. Однако физическая интуиция подсказывает, что вычисление его в пределах от 0 до ¥ неразумно, так как при слишком малых и при слишком больших b мы выходим за границы предположений, которые сформулировали выше. Действительно, при b®0 бессмысленно считать, что электрон после взаимодействия с частицей сохранил свое положение в пространстве: ведь он получает при таком столкновении большую энергию: порядка 2meva2. С другой стороны, при b→∞ энергия, получаемая электроном, оказывается меньше потенциала ионизации и даже меньше порога возбуждения атома. В этом случае предположение о независимых свободных электронах вступает в противоречие с реальной картиной строения вещества. Учет этих соображений дает следующий результат:
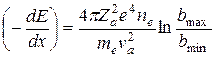 , (19.5)
, (19.5)
где bmin и bmax – минимальное и максимальное значения прицельного параметра, в пределах которых должно проводиться интегрирование. Для получения простейшей оценки тормозной способности отношение прицельных параметров в (19.5) можно заменить отношением максимальной и минимальной энергии, полученной электроном. Тогда
 , (19.6)
, (19.6)
где I – средний потенциал ионизации вещества, обычно определяемый из эмпирически установленного соотношения I = 13,5·Z эВ.
19.3. Релятивистские эффекты. Формула Бете-Блоха и ее анализ. Согласно нерелятивистской теории, максимальный импульс, передаваемый тяжелой частицей отдельному электрону, равен 2meva (ПРИЛОЖЕНИЕ И). Для релятивистской частицы результат будет иным. При релятивистских скоростях движущегося заряда его электрическое поле изменяется: продольное поле, направленное вдоль линии движения частицы, уменьшается пропорционально (1 – β 2), где β = va/c, а поперечное поле увеличивается пропорционально 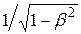 . Продольное сжатие уменьшает эффективное время взаимодействия частицы с электроном, а поперечное нарастание увеличивает кулоновскую силу, действующую на электрон. В результате максимальный импульс, передаваемый электрону, увеличивается в
. Продольное сжатие уменьшает эффективное время взаимодействия частицы с электроном, а поперечное нарастание увеличивает кулоновскую силу, действующую на электрон. В результате максимальный импульс, передаваемый электрону, увеличивается в 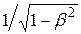 раз, а максимальная кинетическая энергия – в 1/(1 – β 2) раз.
раз, а максимальная кинетическая энергия – в 1/(1 – β 2) раз.
Последовательный учет релятивизма дает для тормозной способности следующий результат:
 . (19.7)
. (19.7)
При va << c формула (19.7) переходит в (19.6), а в релятивистском пределе va → c предсказывает хотя и медленный, но неограниченный рост тормозной способности. В действительности неограниченному росту препятствует эффект плотности – экранировка влияния поля частицы на далекие атомы среды, происходящая благодаря поляризации более близких атомов. Для учета эффекта плотности в формулу (19.7) вводят еще одну поправку δ, явная зависимость которой от характеристик частицы и свойств среды такова, что компенсирует рост ионизационных потерь с увеличением энергии:
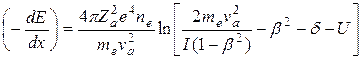 . (19.8)
. (19.8)
В газах эффект плотности невелик, и рост тормозной способности наблюдается до очень высоких энергий. В твердых телах и жидкостях, где плотность электронов велика, он выражен сильнее, и кривая тормозной способности, достигнув минимума при Та ≈ mac2 (где Та кинетическая энергия, ma – массы частицы) далее поднимается незначительно, практически выходя на плато (рис. 19.3).
 Последний член формулы (19.8), обозначенный буквой U, вносит поправку при относительно низкой энергии заряженной частицы. Если ее скорость сравнивается с орбитальной скоростью К- и L-электронов, последние перестают участвовать в соударениях, вследствие чего тормозная способность несколько уменьшается.[163]
Последний член формулы (19.8), обозначенный буквой U, вносит поправку при относительно низкой энергии заряженной частицы. Если ее скорость сравнивается с орбитальной скоростью К- и L-электронов, последние перестают участвовать в соударениях, вследствие чего тормозная способность несколько уменьшается.[163]
Формула (19.8) – основная в теории ионизационного торможения быстрых тяжелых заряженных частиц – называется формулой Бете-Блоха. Отметим, что логарифмический множитель – медленно меняющаяся функция скорости частицы, так что основная зависимость тормозной способности от свойств частицы и вещества определяется выражением, стоящим перед логарифмом. С учетом этого проанализируем формулу Бете-Блоха. Во-первых, можно видеть, что зависимость ионизационных потерь от кинетической энергии и массы частицы сводится к зависимости от их отношения, т.е. скорости. Во-вторых, ионизационные потери пропорциональны квадрату заряда частицы, т.е.
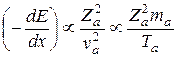 .
.
Это означает, например, что тормозные способности какого-либо вещества для протона и α-частицы при одинаковой скорости этих частиц различаются в 4 раза, а при одинаковой кинетической энергии – в 16 раз.
Ионизационные потери пропорциональны плотности числа электронов в веществе. Обозначим через n0 плотность числа атомов в веществе. Тогда  где Z – атомный номер вещества. Плотность числа атомов связана с массовой плотностью r через массовое число А. Поэтому
где Z – атомный номер вещества. Плотность числа атомов связана с массовой плотностью r через массовое число А. Поэтому
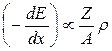 .
.
Учитывая, что отношение Z/A меняется от вещества к веществу в довольно узких пределах (0,5 для гелия и 0,4 для свинца), получаем, что тормозная способность вещества пропорциональна, в основном, его плотности. Вводя определение массовой тормозной способности
 , (19.9)
, (19.9)
видим, что эта величина очень мало меняется от вещества к веществу. Другими словами, потери энергии частицы при прохождении одного и того же слоя xm, выраженного, например, в г/см2, в различных веществах примерно одинаковы.
В заключение отметим, что формула Бете-Блоха остается справедливой до тех пор, пока скорость частицы много больше скорости движения атомных электронов. Как уже отмечалось, в конце пути, когда частица теряет большую часть своей первоначальной энергии, основной вклад в ионизационное торможение вносит перезарядка. Прослеживая мысленно процесс замедления частицы «до конца», мы дойдем до энергий порядка эВ, когда частица уже не может ни ионизировать, ни возбуждать. Дальнейшее замедление таких частиц происходит благодаря упругому рассеянию на атомах и молекулах. Постепенно этот процесс переходит в диффузию, и, в конце концов, попавшие в вещество заряженные частицы включаются в общее тепловое движение атомов.
19.4. Композиционный закон Брэгга. Упругое рассеяние на ядрах. Для того чтобы обобщить формулу Бете-Блоха на тот случай, когда среда, через которую проходит частица, содержит атомы разного сорта, используют т.н. композиционный закон (или правило) Брэгга, сущность которого состоит в следующем. Если вещество представляет собой химическое соединение AmBn из атомов A и B, то его тормозная способность складывается с соответствующими весами из тормозных способностей составляющих его химических элементов:
 . (19.10)
. (19.10)
Обобщение этого правила на любое химическое соединение очевидно. Правило Брэгга вытекает из предположения, что химическая связь между атомами в молекуле не влияет на взаимодействие проходящей через вещество частицы с атомными электронами. В действительности это не так, поскольку атомы вещества, образуя молекулы, всегда в той или иной степени меняют свои индивидуальные свойства. Опыт показывает, что для бинарных соединений AmBn тормозная способность всегда на несколько процентов меньше, чем это следует из композиционного закона. Степень нарушения закона связана с тем, в каком соотношении друг с другом находятся вклады в торможение от электронов внешних оболочек атомов (участвующих в химической связи) и от электронов внутренних оболочек (слабо чувствующих эту связь).
Кулоновское взаимодействие заряженной частицы с атомным ядром может привести к заметному изменению направления ее движения и энергии. Вероятность рассеяния тяжелой заряженной частицы ядром описывается формулой Резерфорда (1.2).[164] Роль упругих соударений растет с ростом массы заряженной частицы и атомного номера вещества. Относительные потери энергии, связанные с рассеянием на ядрах, невелики и уменьшаются с ростом энергии. Так, для протонов с энергией 10 МэВ и 100 МэВ потери энергии на упругое рассеяние в алюминии составляют всего 0,09 и 0,06% от общих потерь соответственно. Однако упругое рассеяние способно привести к заметному искривлению трека частицы.
19.5. Пробег тяжелой заряженной частицы. Связь пробега с энергией.Если пренебречь взаимодействием с атомными ядрами,можно с помощью формулы Бете-Блоха оценить пробег R тяжелой заряженной частицы с начальной скоростью v0 (или энергией Та):

где N0 – число Авогадро, L(va) – логарифмическая функция в формуле (19.8). Пренебрегая этой слабой зависимостью тормозной способности от vа, получаем
 . (19.11)
. (19.11)
Таким образом, пробег частицы обратно пропорционален ее массе и квадрату заряда. Тогда для двух частиц 1 и 2, имеющих одинаковую энергию
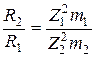 . (19.12)
. (19.12)
Согласно (19.12) пробег протонов и α-частиц одинаковой начальной энергии в одном и том же веществе должен различаться в 16 раз. Сравним это с тем, что дает эксперимент: пробег протонов с энергией 10 МэВ в алюминии составляет 630 мкм, пробег α-частиц той же энергии – около 61 мкм. Их отношение не 16 (около 10,3), но не так уж сильно отличается от этого значения. Учет логарифмической функции L(va) дает результат, еще более близкий к экспериментальному.
Рассмотрим теперь зависимость пробега от природы вещества. Если пренебречь зависимостью от среднего потенциала ионизации, то, согласно (19.11), пробег частицы оказывается обратно пропорциональным массовой плотности вещества. Тогда произведение Rm = Rρ дает пробег, выраженный в массовых единицах (например, г/см2), который в первом приближении не зависит от материала.
Выше уже отмечалось, что траектории тяжелых заряженных частиц в веществе являются почти прямолинейными: вероятность взаимодействия с атомными ядрами весьма мала, а взаимодействие с атомными электронами не приводит к существенному искривлению траектории из-за их малой массы. Экспериментальное определение изменения числа моноэнергетических частиц N в узком пучке[165] приводит к зависимости N от х, изображенной на рис. 19.4. До определенного расстояния x число частиц в пучке постоянно, так как рассеяния на большие углы не происходит. Далее N быстро падает до нуля, т.е. пробеги частиц практически одинаковы. Небольшие колебания пробега связаны со статистическим характером процесса потери энергии. Частицы теряют свою энергию в очень большом, но конечном числе отдельных актов столкновений. Флуктуациям подвержено как число таких актов на единицу пути, так и потеря энергии в каждом отдельном акте. Дифференциальная кривая распределения пробегов 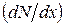 неплохо следует нормальному распределению
неплохо следует нормальному распределению
 .
.
Максимум на дифференциальной кривой отвечает среднему пробегу 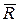 . Экстраполяцией прямолинейного участка интегральной кривой N(x) от точки с абсциссой
. Экстраполяцией прямолинейного участка интегральной кривой N(x) от точки с абсциссой 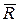 получают экстраполированный пробег Rэ. Величина отклонения от среднего
получают экстраполированный пробег Rэ. Величина отклонения от среднего  для протонов в диапазоне энергий от 1 до 105 МэВ в различных средах составляет 1-2% от
для протонов в диапазоне энергий от 1 до 105 МэВ в различных средах составляет 1-2% от 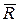 . Для более тяжелых частиц той же энергии эта величина еще меньше.
. Для более тяжелых частиц той же энергии эта величина еще меньше.
Сравнительно небольшие разбросы в длинах пробегов позволяют определять энергии частиц по значениям пробега. Так, на основании массива экспериментальных данных установлены эмпирические соотношения между средним пробегом α-частиц в воздухе при нормальных условиях 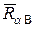 (см) и их энергией Ta (МэВ). Одно из них выглядит так:
(см) и их энергией Ta (МэВ). Одно из них выглядит так:
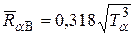 . (19.13)
. (19.13)
Оно выполняется с точностью до 5% для α-частиц с энергией 4-7 МэВ. При меньших энергиях величина пробега оказывается пропорциональной Tα3/4, а при более высоких энергиях Tα2.
 Если известен пробег α-частиц в воздухе, то пробег
Если известен пробег α-частиц в воздухе, то пробег 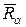 в другой среде может быть найден из равенства пробегов, выраженных в массовых единицах:
в другой среде может быть найден из равенства пробегов, выраженных в массовых единицах:
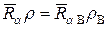 , (19.14)
, (19.14)
где r и rВ – плотности среды и воздуха соответственно. Более точные соотношения учитывают влияние природы вещества. Так, для сложного вещества со средним атомным номером 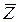 , средней атомной массой
, средней атомной массой 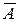 и плотностью r (кг/м3) пробег α-частиц (см)
и плотностью r (кг/м3) пробег α-частиц (см)
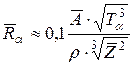 . (19.15)
. (19.15)
19.6. Потери энергии осколками деления.Образующиеся при делении ядер урана или плутония осколки представляют собой многократно заряженные ионы: сразу же после деления они имеют заряд порядка +20e (табл. 19.1). Процесс торможения осколков отличается от торможения в веществе других заряженных частиц, таких, как протоны или α-частицы, которые почти по всей длине пути сохраняют свой заряд. Процесс перезарядки, т.е. захвата и потери электронов этими частицами, существенен лишь в самом конце пути. Напротив, осколки деления в процессе торможения непрерывно меняют свой заряд, а это приводит к тому, что удельные ионизационные потери имеют наибольшее значение в начале пути осколка и монотонно уменьшаются по мере его торможения. Поэтому максимум на кривой Брэгга у осколков деления отсутствует.
Таблица 19.1.
Усредненные по спектру свойства осколков деления
| Осколок | Легкий | Тяжелый |
| Кинетическая энергия, МэВ | ||
| Массовое число | ||
| Заряд ядра | ||
| Заряд иона |
При торможении осколков деления существенное значение приобретают упругие столкновения с ядрами. Это можно пояснить следующим образом. Если принимать во внимание только заряды атомов среды и заряды тормозящихся частиц, то ионизационные потери пропорциональны Zэ2Z, где Zэ – эффективный заряд осколка (в первом приближении это разность заряда ядра осколка и числа электронов в его оболочке, т.е. заряд иона). Потери энергии, обусловленные столкновениями с ядрами, пропорциональны Za2Z2, где Zа – заряд ядра осколка (столкновения осколков с ядрами происходят на таких близких расстояниях, что экранировкой заряда ядра электронной оболочкой можно пренебречь). Следовательно, отношение потерь энергии, обусловленных столкновениями с ядрами, к ионизационным потерям оказывается пропорциональным (Za/Zэ)2Z. Для протонов и α-частиц (Za/Zэ)2 = 1, а для осколков деления даже в начале пути (Za/Zэ)2 ≈ 4; к концу пути эта величина увеличивается в сотни раз. Из-за сравнительно большой вероятности упругого рассеяния на ядрах для осколков деления среднеквадратичный угол рассеяния больше, чем для протонов и α-частиц. По этой же причине треки осколков деления сопровождаются короткими треками ядер отдачи с большой плотностью ионизации.
Дата добавления: 2020-12-11; просмотров: 526;











