Теорема 2 (о строении обратной матрицы).

Элементы обратной матрицы равны: .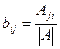

Доказательство.Умножим транспонированную матрицу, составленную из алгебраических дополнений, на А.

.

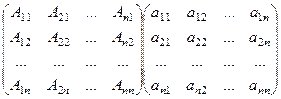Рассмотрим подробно элемент с индексами 1,1.

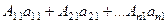, это разложение 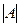по 1 столбцу.

По диагонали получатся элементы вида 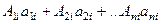,все равные .

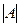На всех местах кроме диагонали, получим 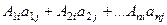, то есть произведения элементов столбца j на алгебраические дополнения элементов другого столбца, i-го. В силу теоремы 2 из прошлого параграфа, они равны 0.

Итак, произведение матриц получилось следующее:

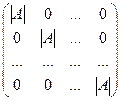.Если разделить на 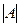, то получим матрицу .

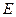Таким образом, обратная матрица имеет вид:

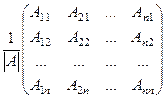, т.е. её элементы равны: .

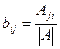(Что и требовалось доказать).

Алгоритм нахождения 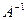можно разделить на 5 мелких шагов:

1. Проверить невырожденность с помощью определителя.

2. Составить матрицу из дополняющих миноров M_ij.

3. Изменить знаки в шахматном порядке, то есть домножить на (-1)^i+j, где i,j - номера строки и столбца. Получатся алгебраические дополнения A_ij.

4. Транспонировать полученную матрицу.

5. Поделить на определитель исходной матрицы.

(шаги 3 и 4 перестановочны).

Пример.Найти .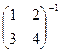

Решение. 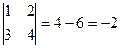. Вывод: 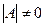, существует обратная матрица.

Матрица из миноров: .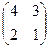

Матрица из алг. дополнений: .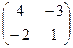

Транспонируем её: .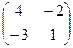

Делим её на определитель, и записываем ответ: = .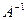

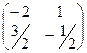Можно сделать проверку: = .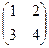

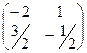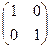Лекция 6. 28.11.2020.

Пример (3 порядка).Найти обратную матрицу: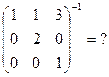

Решение. 1) 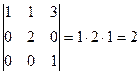. 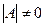, существует .

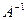2) Запишем матрицу, состоящую из всех возможных миноров 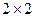, которых существует 9 штук: = .

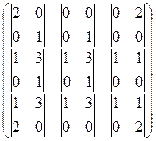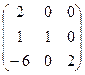3) Матрица из алгебраических дополнений: .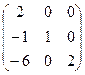

(т.е. в шахматном порядке изменили знаки, там где сумма номеров строки и столбца нечётна).

Транспонируем её: 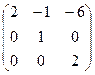. Делим на определитель, равный 2, итог: = .

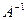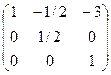§ 4. Ранг матрицы.Теорема о ранге матрицы.

Лекция 7. 30.11.2020.