Кинематика поступательного и вращательного движений материальной точки
Механическим движением тел называют изменение их положения (или положения их частей) в пространстве с течением времени. В основе классической механики лежат законы Ньютона.
Кинематика изучает механическое движение с геометрической точки зрения и не рассматривает причины, вызывающие это движение. В механике рассматривается движение таких объектов, как материальная точка и абсолютно твердое тело.
Материальной точкой называется тело, размерами которого в данных условиях можно пренебречь.
Абсолютно твёрдым телом называется тело, деформацией которого в данных условиях можно пренебречь. Абсолютно твёрдое тело можно рассматривать как систему материальных точек, жестко связанных между собой.
1.1. Кинематические характеристики движения материальной точки
Описать движение материальной точки – значит знать ее положение относительно выбранной системы отсчета в любой момент времени. Системойотсчёта называется система координат, связанная с телом отсчёта и снабжённая синхронизированными часами. Наиболее часто используется прямоугольная декартова система координат (рис. 1).
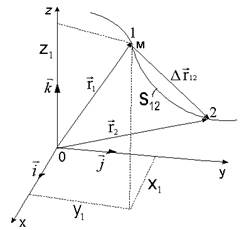
| Положение материальной точки характеризуется радиусом-вектором 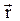 , проведённым из начала координат в данную точку (рис. 1). Проекции радиуса-вектора на координатные оси соответствуют координатам точки в выбранной системе координат (рис. 1): , проведённым из начала координат в данную точку (рис. 1). Проекции радиуса-вектора на координатные оси соответствуют координатам точки в выбранной системе координат (рис. 1):
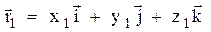 .
Движение материальной точки задано, если известна зависимость координат точки от времени, т.е. .
Движение материальной точки задано, если известна зависимость координат точки от времени, т.е.
|
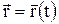 или
или 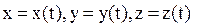 .
.
Данные уравнения являются кинематическими уравнениями движения материальной точки, или законом движения точки. В процессе движения конец радиуса-вектора, связанный с точкой, описывает в пространстве кривую, называемую траекторией движения материальной точки. В зависимости от формы траектории различают прямолинейное и криволинейное движения.
Перемещением материальной точки называют вектор, проведённый из начальной точки в конечную точку траектории (рис. 1):

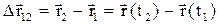 .
.
Вектор 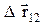 может быть выражен через приращения координат и орты соответствующих осей (единичные векторы, направленные по осям):
может быть выражен через приращения координат и орты соответствующих осей (единичные векторы, направленные по осям):
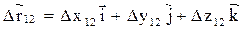 .
.
Модуль вектора перемещения можно определить следующим образом:
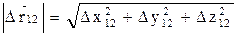 .
.
Путь материальной точки S12 - это длина траектории.
Скорость - векторная физическая величина, характеризующая быстроту изменения положения тела в пространстве, равная перемещению тела за единицу времени. Различают среднюю и мгновенную скорости.
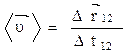 - средняя скорость;
- средняя скорость;
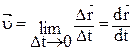 - мгновенная скорость;
- мгновенная скорость;
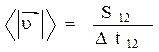 - среднее значение модуля скорости.
- среднее значение модуля скорости.
Вектор средней скорости направлен так же, как и вектор перемещения 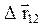 . Вектор мгновенной скорости направлен по касательной к траектории движения так же, как вектор элементарного перемещения:
. Вектор мгновенной скорости направлен по касательной к траектории движения так же, как вектор элементарного перемещения: 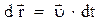 . Так как
. Так как 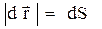 , где dS - элементарный путь, то модуль мгновенной скорости равен производной пути по времени:
, где dS - элементарный путь, то модуль мгновенной скорости равен производной пути по времени:
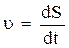 .
.
В декартовой системе координат скорость можно представить через её проекции на оси:
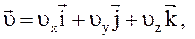
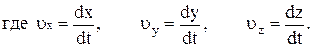
Модуль скорости может быть найден по следующей формуле:
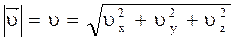 .
.
При рассмотрении движения тела относительно двух различных инерциальных систем отсчета используют классический закон сложения скоростей: скорость тела относительно неподвижной системы отсчета 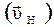 равна векторной сумме скорости тела относительно движущейся системы
равна векторной сумме скорости тела относительно движущейся системы 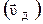 и скорости самой движущейся системы относительно неподвижной
и скорости самой движущейся системы относительно неподвижной 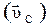 :
:
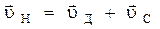 .
.
Ускорение - векторная физическая величина, характеризующая быстроту изменения скорости с течением времени, равная приращению скорости за единицу времени. Различают среднее и мгновенное ускорения.
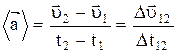 - среднее ускорение,
- среднее ускорение,
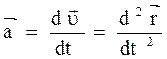 - мгновенное ускорение.
- мгновенное ускорение.
Вектор ускорения может быть представлен через его проекции на координатные оси:
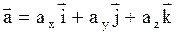 ,
,
где 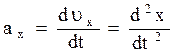 ,
, 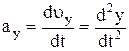 ,
, 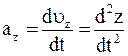 .
.
Модуль ускорения можно определить следующим образом:
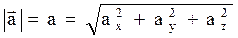 .
.
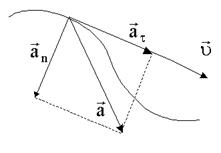
1.2. Тангенциальная и нормальная составляющие ускорения
Часто используется представление ускорения через две составляющие: тангенциальное и нормальное ускорения (рис. 2):
Рис. 2 |
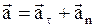 ; ;
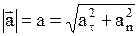 . .
|
Тангенциальное ускорение характеризует изменение скорости по модулю (величине) и направлено по касательной к траектории:
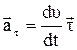 ,
,
где 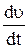 - производная модуля скорости,
- производная модуля скорости, 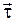 - единичный вектор касательной, совпадающий по направлению со скоростью.
- единичный вектор касательной, совпадающий по направлению со скоростью.
Нормальное ускорение характеризует изменение скорости по направлению и направлено по радиусу кривизны к центру кривизны траектории в данной точке:
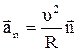 ,
,
где R - радиус кривизны траектории, 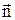 - единичный вектор нормали.
- единичный вектор нормали.
Модуль вектора ускорения может быть найден по формуле
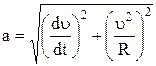 .
.
1.3. Основная задача кинематики
Основная задача кинематики заключается в нахождении закона движения материальной точки. Для этого используются следующие соотношения:
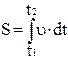 ;
; 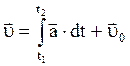 ;
; 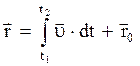 ;
; 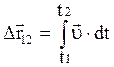 ;
;
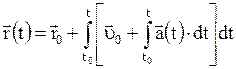 .
.
Частные случаи прямолинейного движения:
1) равномерное прямолинейное движение: 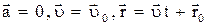 ;
;
2) равнопеременное прямолинейное движение: 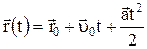 .
.
Дата добавления: 2019-05-21; просмотров: 620;