МОСТЫ С РАДИАЛЬНО-ВАНТОВЫМИ ФЕРМАМИ

(висячей системы)

Общие сведения

Мосты с радиально-вантовыми фермами висячей системы предложены французским архитектором и инженером Пойе в 1790 г.г. см. рис. 9.4.

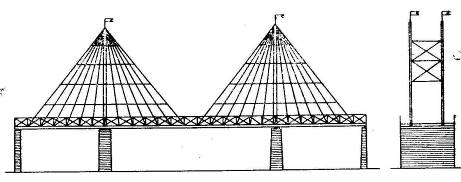
Рис. 9.4. Проект моста системы Пойе

В XVIII, начале XIX в.в. происходило большое количество обрушений этих конструкций связанное с сильным провисанием вант и значительными деформациями системы.

Инженерные разработки вантовых ферм в начале ХХ в проводились французским инженером Жискляром, рассматривавшим работу радиально-вантовых ферм под легкими нагрузками. Детальные теоретические исследования вантовых ферм с предложением новых систем проводил И.М. Рабинович.

Область применения вантовых ферм – перекрытие пролетов величиной до 200 … 250 м.

Геометрическая неизменяемость

Вантовая ферма (рис. 9.5) представляет собой геометрически неизменяемую систему, в стержнях которой, при любых возможных сочетаниях расчетных нагрузок, могут возникать лишь растягивающие усилия, что позволяет осуществлять, их из гибких элементов (стальных канатов или тросов).

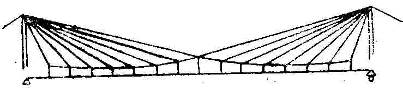
Рис. 9.5. Общий вид вантовой фермы

Как известно, в вантовых фермах ряд стержней имеет двухзначные линии влияния (рис. 9.6). Если при загружении отрицательных участков линии влияния временной нагрузкой, допустить возможность превышения сжимающего усилия в стержне над растягивающим усилием от загружения постоянной нагрузкой всей линии влияния и, в то же время сохранить этот стержень гибким, то он выйдет из работы, а вантовая ферма утратит геометрическую неизменяемость и получит большой прогиб.

Так как этого допустить нельзя, то необходимо обеспечить растягивающее усилие в каждом гибком стержне фермы, при самом неблагоприятном сочетании расчетных нагрузок.

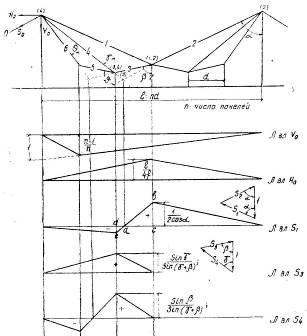
Рис. 9.6. Линии влияния в стержнях вантовой фермы

Учитывая возможность некоторых отклонений действительной, работы фермы от принятых в расчете предпосылок, требуется обеспечить в каждом гибком стержне с двухзначной линией влияния известный «запас по растяжению».

Число раз, в которое нужно увеличить временную нагрузку, поставленную по длине отрицательных участков линии влияния, чтобы полное усилие в стержне с учетом постоянной нагрузки стало равным нулю, называется коэффициентом, запаса по растяжению.

Приведенное определение выражается условием: ;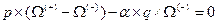

здесь:

р – постоянная распределенная нагрузка на п.м. фермы;

q – временная распределенная нагрузка на п.м. фермы;

W⁽⁺⁾ – площадь положительных участков линии влияния;

W^(-) – площадь отрицательных участков;

a – коэффициент запаса по растяжению.

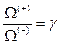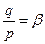Из написанного условия, обозначив: и получим: .

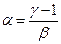Этот коэффициент запаса назначают обычно в пределах 1,5 … 1,75.

Для строгого удовлетворения требованиям геометрической неизменяемости, все стержни вантовой фермы должны быть прямолинейными. В действительности, стержни, особенно длинные и пологие, провисают от собственного веса, причем величина провеса изменяется с изменением усилия, этот недостаток вызывает увеличение вертикального прогиба системы под временной нагрузкой, а для его уменьшения избегают устройства длинных вант, или вводят в конструкцию фермы специальные поддерживающие кабели и подвески.

Прогиб

Ограничение прогиба от временной вертикальной нагрузки является одним из основных требований, предъявляемых ко всякому пролетному строению. Для вантовых мостов это требование, может явиться определяющим при выборе материала ферм и назначении допускаемых напряжений. Наибольший допустимый прогиб пролетных строений обычно нормируется величиною отношения его к пролету ферм.

Наибольший прогиб вантовых ферм d возникает в середине пролета, при загружении всего пролета временной нагрузкой. Он может быть вычислен по формуле:

;

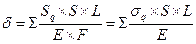здесь:

S_q – усилия в элементах от расчетной временной нагрузки, при загружении всего пролета;

S – усилия в тех же элементах, от единичной вертикальной сосредоточенной силы Р = 1, приложенной в середине пролета;

L, Е, F – длины, модули упругости и площади поперечных сечений соответствующих элементов моста;

s_q – напряжения в элементах от временной нагрузки.

Знак суммы распространяется на все стержни фермы, а также удерживающие ванты (оттяжки) и пилоны моста.

Таким образом, выражение для d показывает, что прогиб вантовой фермы от временной нагрузки уменьшается:

– с уменьшением напряжений в вантах;

– с увеличением модуля упругости вант;

– с уменьшением отношения временной нагрузки фермы к постоянной.

Прогиб фермы является также функцией величины отношения стрелы фермы к пролету, так как от этой величины зависят усилия в вантах и длины вант.

Наивыгоднейшее значение отношения f/L находится в пределах 1/6 … 1/8. Повышение этого отношения связано с увеличением высоты пилонов и удорожанием сооружения.

Модуль упругости троса, идущего для изготовления вант, составляет 1,5´10⁶ … 1,6´10⁶ кг/см². Значение модуля можно увеличить до 1,8´10⁶ кг/см², если трос, перед употреблением в дело, подвергнуть предварительному растяжению, в течение 1 … 1,5 часов до напряжений, превышающих в 1,5 раза расчетное.

Уменьшения, прогибов вантовых ферм можно достичь, снижением напряжений в вантах, или увеличением собственного веса проезжей части, однако оба эти приема связаны с существенным удорожанием стоимости моста.

В связи с этим норму максимально допускаемого прогиба для вантовых мостов увеличивают сравнительно с установленными нормами для мостов балочных и арочных, и по опыту проектирования и эксплуатации, принято считать допускаемым прогиб этих сооружений в 1/300 … 1/500 пролёта.

Вес

Полный вес вантовых ферм с подвесками и удерживающими вантами может быть ориентировочно определен по формуле инженера Е.И. Крыльцова (Крыльцов Е.И. Вантовые мосты. – М.: Трансжелдориздат, 1935 г.):

,

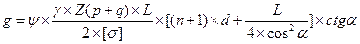здесь:

g – вес вантовой фермы;

y – конструктивный коэффициент (отношение действительного веса фермы к теоретическому), равный 1,4 … 1,6;

g – удельный вес материала ферм;

n – число панелей в полу пролете;

a – величина панели. Остальные обозначения см выше.

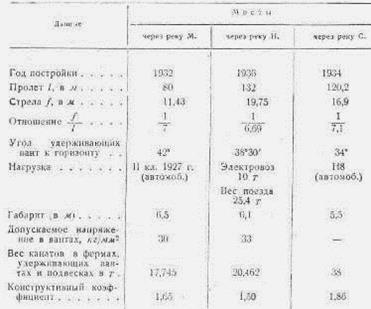
В таблице 9.1 представлены некоторые данные о вантовых мостах, построенных в СССР.

Табл. 9.1.