Проверка гипотез о различиях
Существует множество вариантов статистических проверок гипотез о различиях переменных или групп. Процедуры проверки этих гипотез можно в общем виде классифицировать на параметрические и непараметрические, исходя из шкалы измерения переменных.
Параметрические методы проверки гипотез (parametric tests) предполагают, что изучаемые переменные измерены с помощью интервальной шкалы.
Непараметрические методы проверки гипотез (nonparametric tests) предполагают, что переменные измерены с помощью номинальной или порядковой шкал.
Дальнейшая классификация проводится в зависимости от количества исследуемых выборок: одна, две или больше. При этом, число выборок определяют, исходя из метода дальнейшей обработки данных для анализа, а не из того, как были собраны данные.
Выборки считаются независимыми в том случае, если взяты случайным образом из различных генеральных совокупностей. Для анализа данные, принадлежащие различным группам респондентов, например мужчинам и женщинам, обычно обрабатывают как независимые выборки. С другой стороны, выборки являются парными (связанными),когда данные двух выборок имеют отношение к одной и той же группе респондентов.
Наиболее популярный параметрический критерий для проверки гипотез о равенстве средних заключается в расчете значений t-статистики.
Т-статистика (t-statistic) подразумевает, что переменная нормально распределена, среднее известно (или предполагается, что оно должно быть известно) и дисперсия генеральной совокупности определена по данным выборки.
Процедура t-проверки гипотезы для независимых выборок состоит из следующих этапов.
1. Сформулировать нулевую Но и альтернативную Hα гипотезы.
2. Выбрать соответствующую формулу для вычисления t-статистики.
3. Выбрать уровень значимости а для проверки нулевой гипотезы Но. Обычно выбирают уровень значимости α, равный 0,05.
4. Взять одну или две выборки и для каждой вычислить значение средней и стандартное отклонение.
5. Вычислить значение t-статистики, приняв, что нулевая гипотеза Но верна.
6. Вычислить число степеней свободы и оценить вероятность получения большего значения статистики из Таблицы 3 Приложения. (Альтернативно, вычислить критическое значение t-статистики).
7. Если вероятность, рассчитанная на этапе 6 меньше, чем уровень значимости α, выбранный на этапе 3, то отклонить нулевую гипотезу Но. Если значение вероятности больше, то Но не отклонять.
8. Выразить полученный результат с точки зрения решения проблемы маркетингового исследования.
Проиллюстрируем общую процедуру t-проверки гипотез на следующем примере. Предположим, что производитель пряников разработал новый рецепт и рассматривает два вида упаковки новых пряников. Компания проводит эксперимент, в рамках которого пряники в упаковке А поступают в 10 магазинов, выбранных случайным образом. Пряники в упаковке В поступают в другие 10 магазинов, составляющие вторую независимую выборку. Результаты эксперимента, проводившегося в течение месяца, представлены в таблице.
| Магазин | Упаковка А | Упаковка В |
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - | ||
| - |
Среднее продаж пряников в упаковке А составляет 403 упаковки на магазин, а в упаковке В – 390,3. Можно ли утверждать, что компания должна выбрать упаковку А? Этот вывод можно проверить с помощью t-критерия.
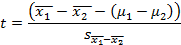
где 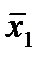 - выборочное среднее для первой выборки магазинов,
- выборочное среднее для первой выборки магазинов, 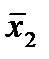 - выборочное среднее для второй выборки,
- выборочное среднее для второй выборки, 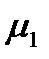 - генеральное среднее для первой выборки магазинов,
- генеральное среднее для первой выборки магазинов, 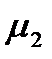 - генеральное среднее для второй выборки, а
- генеральное среднее для второй выборки, а 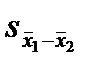 . – оценка ошибки статистики.
. – оценка ошибки статистики.
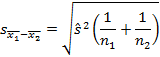
где 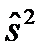 - объединенная выборочная дисперсия (предполагается, что две дисперсии двух родительских совокупностей равны),
- объединенная выборочная дисперсия (предполагается, что две дисперсии двух родительских совокупностей равны), 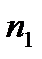 - размер выборки для первой группы магазинов,
- размер выборки для первой группы магазинов, 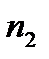 - размер выборки для второй группы. В свою очередь
- размер выборки для второй группы. В свою очередь 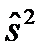 рассчитывается как:
рассчитывается как:
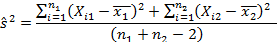
где 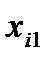 - значение Х для i-го элемента выборки в первой группе магазинов,
- значение Х для i-го элемента выборки в первой группе магазинов, 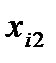 - значение Х для i-го элемента выборки во второй группе.
- значение Х для i-го элемента выборки во второй группе.
Нулевая и альтернативная гипотезы формулируются следующим образом:
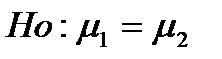
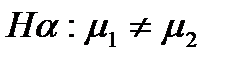
Применяя эти формулы к данным, полученным в ходе эксперимента, объединенную выборочную дисперсию можно найти следующим образом:
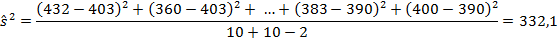
Оценка ошибки статистики:
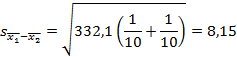
Расчетное t составит:
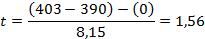
Полученное значение t необходимо сопоставить с t-таблицей для 18 степеней свободы, чтобы определить статистическую значимость результатов. В данном случае критическое значение t, соответствующее двусторонней проверке и уровню значимости 0,05, равно 2,101. Поскольку расчетное t меньше критического значения, мы не можем отвергнуть нулевую гипотезу о том, что генеральные средние равны.
В качестве непараметрического метода проверки гипотез, рассмотрим проверку Колмогорова-Смирнова
В рамках данной проверки также используется сравнение наблюдавшихся и ожидаемых частот для определения того, находятся ли наблюдавшиеся результаты в согласии с заявленной нулевой гипотезой; используется также для определения того, взяты ли две независимые выборки из одной и той же генеральной совокупности или из совокупности с тем же распределением. В проверке Колмогорова-Смирнова используются, как правило, порядковые данные.
Рассмотрим, например, производителя кофе, который проверяет четыре различных степени крепости кофе. Поставлена задача определить, существует ли какое либо различие в предпочтении крайностей. Если таковое существует, то компания будет производить только предпочтительные степени крепости. В противном случае будут производиться все четыре степени крепости. Нулевая гипотеза, которая подлежит проверке, заключается в том, что предпочтение степени крепости отсутствует.
Для начала необходимо рассмотреть эмпирическое распределение предпочтений и сравнить его с теоретическим. Для удобства сравнения сведем данные в таблицу наблюдавшегося и теоретического кумулятивного распределения предпочтений.
| Степень крепости кофе | Наблюдавшееся число | Наблюдавшаяся доля | Кумулятивная доля | Теоретическая доля | Теоретическая кумулятивная доля |
| Очень крепкий | 0,30 | 0,30 | 0,25 | 0,25 | |
| Крепкий | 0,50 | 0,80 | 0,25 | 0,50 | |
| Средний | 0,15 | 0,95 | 0,25 | 0,75 | |
| Легкий | 0,05 | 1,00 | 0,25 | 1,00 |
Критерий Колмогорова-Смирнова основан на максимальном значении абсолютной разности между 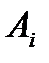 и
и 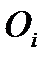 . Значение критерия вычисляют по формуле:
. Значение критерия вычисляют по формуле:
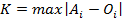
где 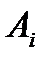 - обозначает кумулятивную частость для каждой категории теоретического (предполагаемого) распределения, а
- обозначает кумулятивную частость для каждой категории теоретического (предполагаемого) распределения, а 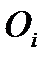 сравниваемое значение наблюдавшейся частости.
сравниваемое значение наблюдавшейся частости.
Полученное значение критерия сравнивают с величиной D, которая при α=0,05 для больших выборок задается как:
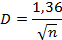
где n- объем выборки.
В нашем случае объем выборки равен 100, D=0,136, а K=(0,80-0,50)=0,30. Расчетное значение К превышает D и, таким образом, нулевая гипотеза об отсутствии предпочтений степени крепости отвергается. Данные указывают на статистически значимое предпочтение более крепкого кофе.
Выше нами были рассмотрены методы проверки различий между двумя средними или двумя медианами разных выборок. Если маркетолог имеет дело с большим числом средних или медиан, то необходимо применять методы дисперсионного и ковариационного анализа.
Дисперсионный и ковариационный анализ используется для изучения различий средних значений зависимых переменных, вызванных влиянием контролируемых независимых переменных, при условии, что учтено влияние неконтролируемых независимых переменных.
Дисперсионный анализ применяют как проверку статистической значимости различий выборочных средних для двух или больше совокупностей. Обычно нулевая гипотеза утверждает, что все выборочные средние равны. Например, исследователю интересно узнать, действительно ли люди с различным уровнем потребления какого-либо продукта (например, молока) различаются предпочтением к конкретной марке продукта (например, марке «Простоквашино») измеренным по девятибалльной шкале Лайкерта. Проверку нулевой гипотезы, утверждающей, что группы потребителей, выделенные по признаку интенсивности потребления молока, не различаются предпочтением к марке «Простоквашино», можно выполнить, используя дисперсионный анализ.
В своей простейшей форме дисперсионный анализ должен иметь зависимую переменную (предпочтение к марке «Простоквашино»), которая является метрической (измеренной с помощью интервальной или относительной шкалы). Кроме того, должна быть одна или больше независимых переменных (в нашем примере – потребление продукта: сильное, среднее, слабое и отсутствие потребления).
Если все переменные независимые, то их изучают методом ковариационного анализа. Он представляет собой специальный метод анализа дисперсий, в котором эффекты одной или больше сторонних переменных, выраженных в метрической шкале, удаляют из зависимой переменной перед выполнением дисперсионного анализа.
Например, ковариационный анализ необходим, если исследователь хочет изучить предпочтения пользователей в группах с различным уровнем потребления и уровнем лояльности, приняв во внимание отношение респондентов к составу продуктов питания (например, содержанию жира в молоке) и к воспринимаемой важности этих продуктов для поддержания здоровья.
Регрессионный анализ объясняет вариацию в завоеванной доле рынка, продажах, предпочтении торговой марки и других маркетинговых результатах, получаемых при управлении такими маркетинговыми переменными, как реклама, цена, распределение и качество продукции.
Регрессионный анализ представляет собой статистический метод установления формы и изучения связей между метрической зависимой переменной и одной или несколькими независимыми переменными. Выделяют простой и множественный регрессионный анализ.
Контрольные вопросы и вопросы для самостоятельного изучения
1. Чем отличается таблица распределения частот от таблицы сопряженности?
2. Какое общее правило вычисления процентов при перекрестной табуляции?
3. Что означает подавленная связь между переменными? Как ее выясняют?
4. Чем отличаются параметрические и непараметрические методы проверки гипотез?
5. В чем состоят сходства и различия между дисперсионным и ковариационным анализом?
6. Какая связь между дисперсионным анализом и проверкой гипотез с помощью t-критерия?
Дата добавления: 2020-11-18; просмотров: 742;











